Anstieg (Physik)

Anmelden

Anstieg (Physik)

Anstieg

Bei einer Geraden können wir den Anstieg des Graphen mit einem Steigungsdreieck bestimmen. Ein Steigungsdreieck ist immer rechtwinklig und wird direkt an die Gerade angelegt.
Zwei Geraden in einem s(t)-Diagramm. Auf der horizontalen Achse wird die Zeit in Sekunden, auf der vertikalen Achse der Weg in Metern angegeben. An beiden Geraden ist ein Steigungsdreieck eingezeichnet. WĂ€hrend die rote gerade innerhalb einer Sekunde um 2 Meter ansteigt (Anstieg = 2), steigt die blaue Gerade in 4 Sekunden 3 Meter an (Anstieg = 3/4).
§

© Digitale Lernwelten

ArrcBYSA

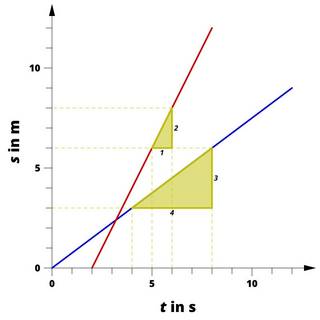
Mithilfe des Steigungsdreiecks kann der Anstieg einer Geraden bestimmt werden.

Um den Anstieg der roten Geraden zu bestimmen, gehen wir auf der horizontalen Achse eine Einheit nach rechts und anschließend zwei Einheiten nach oben. Der Anstieg der Graden ist 2 m/s.

FĂŒr den Anstieg der blauen Geraden gehen wir 4 Einheiten nach rechts und anschließend 3 Einheiten nach oben. Der Anstieg betrĂ€gt somit 3/4 m/s (oder 0,75 m/s).

Position und GrĂ¶ĂŸe des Steigungsdreiecks machen bei einer Geraden keinen Unterschied. Wenn wir bei der roten Gerade zwei Einheiten nach rechts gehen, so sind es 4 Einheiten nach oben, der Anstieg bleibt derselbe.
Eine Gerade in einem s(t)-Diagramm. Der Körper bewegt sich rĂŒckwĂ€rts, der Anstieg ist negativ. Das Steigungsdreieck zeigt, dass die Gerade innerhalb von 2 Sekunden um einen Meter abfĂ€llt (Anstieg = -1/2).
§

© Digitale Lernwelten

ArrcBYSA

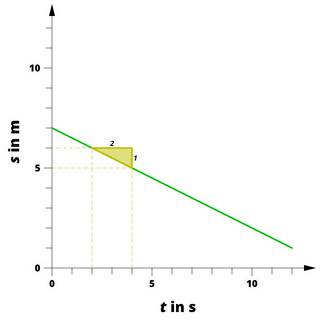
Der Anstieg kann auch negativ sein.

Der Anstieg einer Geraden kann auch negativ sein. In diesem Beispiel betrÀgt der Anstieg der Geraden - 1/2 m/s (oder -0,5 m/s).