Im vorigen Modul hast du gelernt, wie du gleichförmige geradlinige Bewegungen beurteilen und ihre Geschwindigkeit berechnen kannst. Doch im Alltag findest du viele Beispiele für Körper, die sich nicht geradlinig oder nicht gleichförmig bewegen.
In diesem Kapitel lernst du weitere Bewegungsformen kennen und wie du diese beurteilen kannst.

§
Urheber: Christian Mikhael
Unsplash
2. Bewegungsformen
2.1 Bahnformen
Bislang hast du dir lediglich geradlinige, gleichförmige Bewegungen angesehen.
- Geradlinig heißt, dass die Bewegung entlang einer Geraden erfolgt (auch „lineare Bewegung“ oder „eindimensionale Bewegung“ genannt).
- Gleichförmig heißt, dass sich der Körper innerhalb eines Zeitraums immer mit derselben Geschwindigkeit bewegt (also z. B. nicht beschleunigt oder bremst).
Die Bahnform bezeichnet die Bahn, entlang der sich der Körper bewegt. Es gibt auch Bewegungen, bei der die Bahn keine Gerade ist. Schau dir die folgenden Bahnformen an:
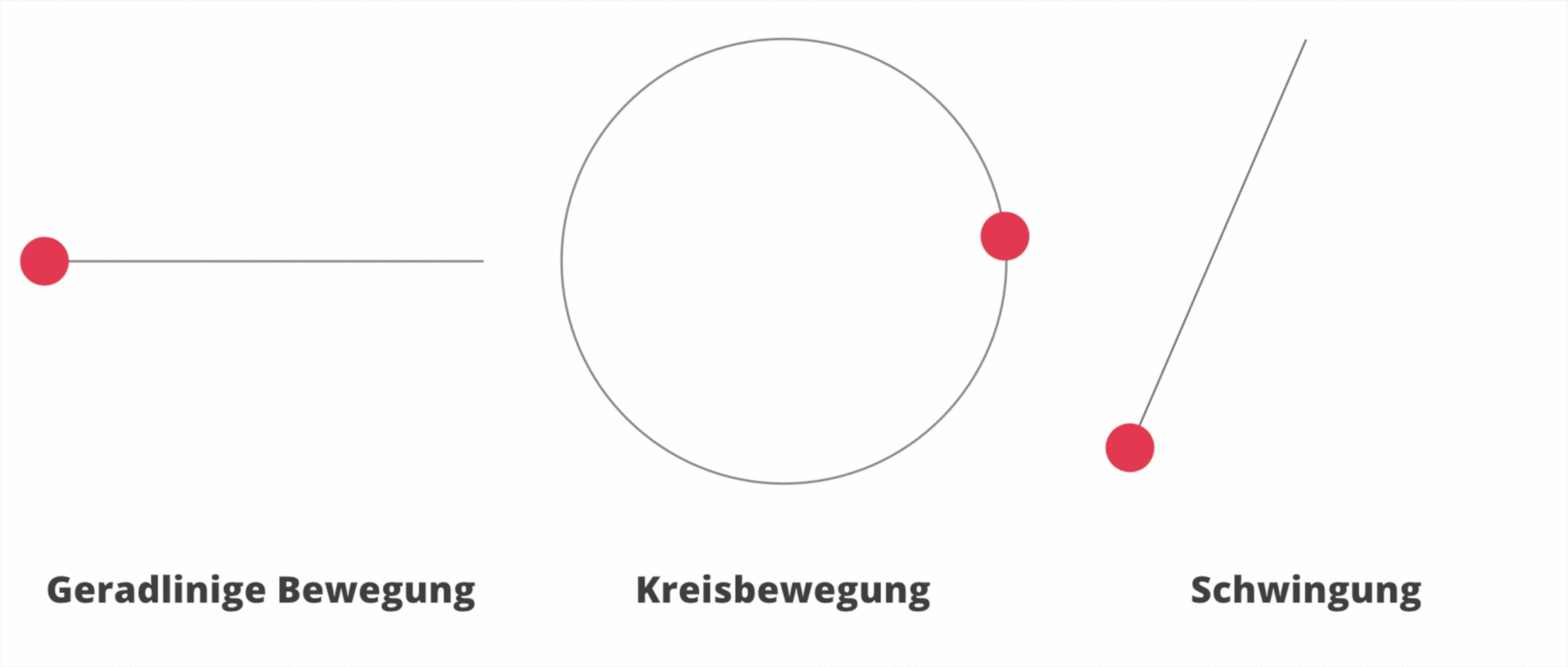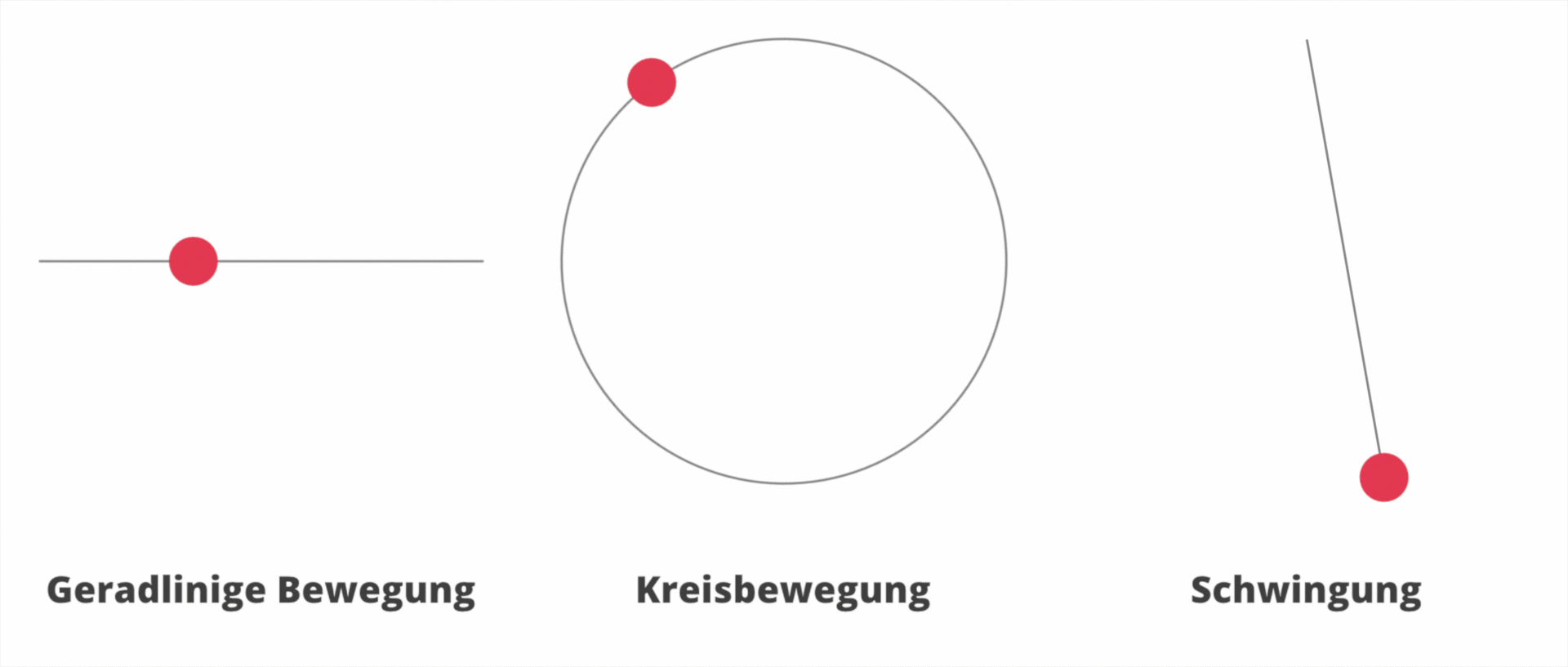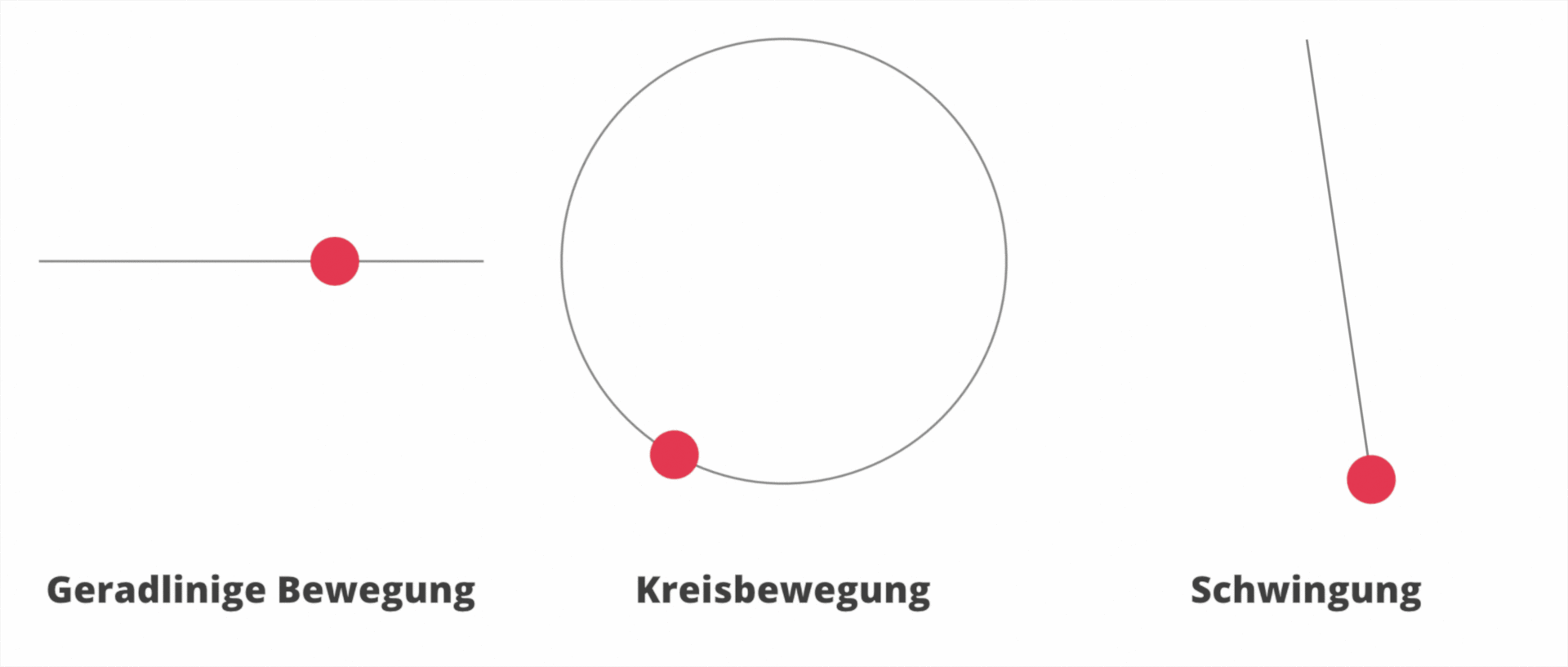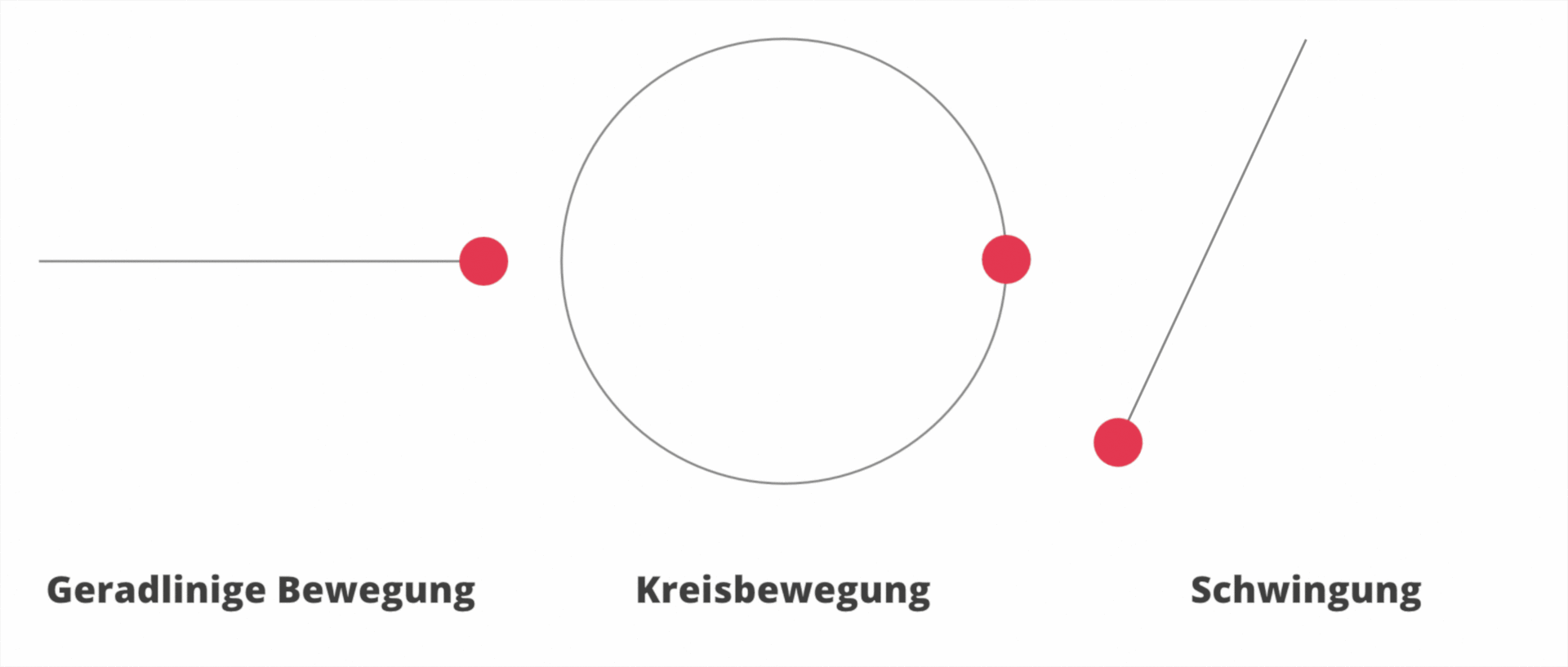
§
Urheber: Digitale Lernwelten GmbH
Ein Körper bewegt sich immer entlang einer Bahn. Bewegungen können unterschiedliche Bahnformen haben.
In der Natur und im Alltag findest du viele Beispiele für unterschiedliche Bahnformen. Wenn du schon einmal in einem Freizeitpark warst, kommen dir bestimmt die folgenden Beispiele bekannt vor.
Aufgabe A – Besuch im Freizeitpark
Betrachte die Attraktionen im Freizeitpark und wähle die jeweilige Bahnform aus.
Aufgabe B – Bahnformen im Alltag
Überlege dir mindestens ein weiteres Beispiel für jede der folgenden Bahnformen (es muss keine Freizeitparkattraktion sein):
- Geradlinige Bewegung
- Kreisbewegung
- Schwingung
Tausche dich mit deinen Mitschülern über deine Ergebnisse aus und erstelle eine gemeinsame Liste mit Beispielen.
Hintergrund
Das Bezugssystem
Hintergrund
Das Bezugssystem
Das Bezugssystem
Ruf dir noch einmal den ersten Satz zu Beginn des Moduls in Erinnerung: „Wir befinden uns ständig in Bewegung.“ Auch dann, wenn wir uns selbst gar nicht bewegen. Denn die Erde bewegt sich kontinuierlich und annähernd kreisförmig um die Sonne. Doch warum musste diese Bewegung bei den bisherigen Beurteilungen und Berechnungen nicht berücksichtigt werden?
Dafür gibt es das sogenannte Bezugssystem. Das Bezugssystem gibt an, von wo aus die Bewegung betrachtet wird.

§
© Urheber Planet Erde: The New York Public Library (https://unsplash.com/photos/yEauzeZU6xo); Urheber Bus Straßenkreuzung: Erik Mclean (https://unsplash.com/photos/od3m5BaHpKc); Urheber Bus innen: Ant Rozetsky (https://unsplash.com/photos/lr9vo8mNvrc); Komposition: Digitale Lernwelten
Das Bezugssystem gibt an, von wo aus die Bewegung betrachtet wird.
Betrachte als Beispiel einen Schüler, der sich durch den Bus zu einem Sitzplatz bewegt.
- Betrachtest du die Bewegung aus dem Weltraum, müssen die Bewegungen der Erde, des Busses und des Schülers berücksichtigt werden.
- Betrachtest du die Bewegung auf der Erde, müssen nur noch die Bewegungen des Busses und des Schülers berücksichtigt werden.
- Befindest du dich selbst im Bus, muss lediglich die Bewegung des Schülers betrachtet werden.
Somit ergibt sich endlich die vollständige Definition der Bewegung:
Ein Körper ist dann in Bewegung, wenn er seinen Ort mit der Zeit relativ zu seinem Bezugssystem ändert.
Bonusaufgabe – Bezugssystem
Schau dir noch einmal das vorige Modul an. Von welchem Bezugssystem wurde bislang immer ausgegangen?
2.2 Ungleichförmige Bewegungen
In der Natur bewegen sich nahezu alle Körper ungleichförmig. Zwar kann sich ein Fahrrad, Auto, Zug oder Flugzeug über einen längeren Zeitraum mit derselben Geschwindigkeit bewegen – sie alle müssen dennoch zuerst einmal beschleunigen und irgendwann wieder abbremsen.
§
Urheber: Digitale Lernwelten GmbH
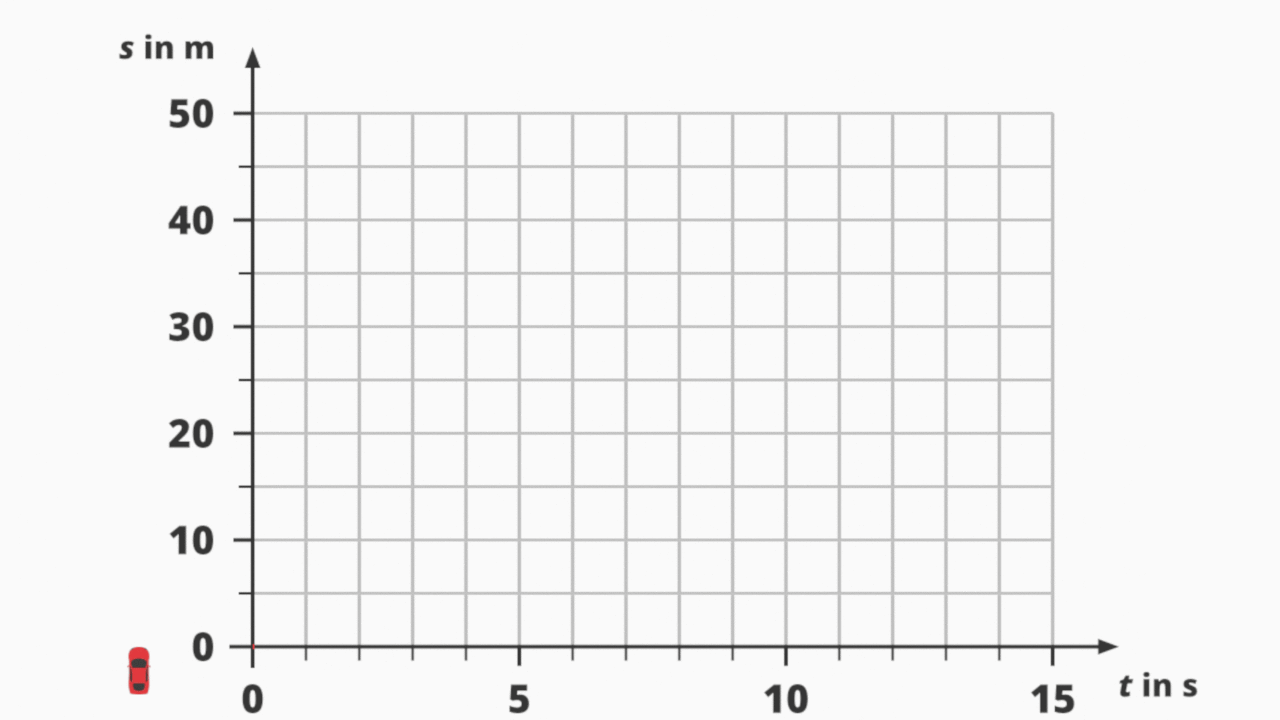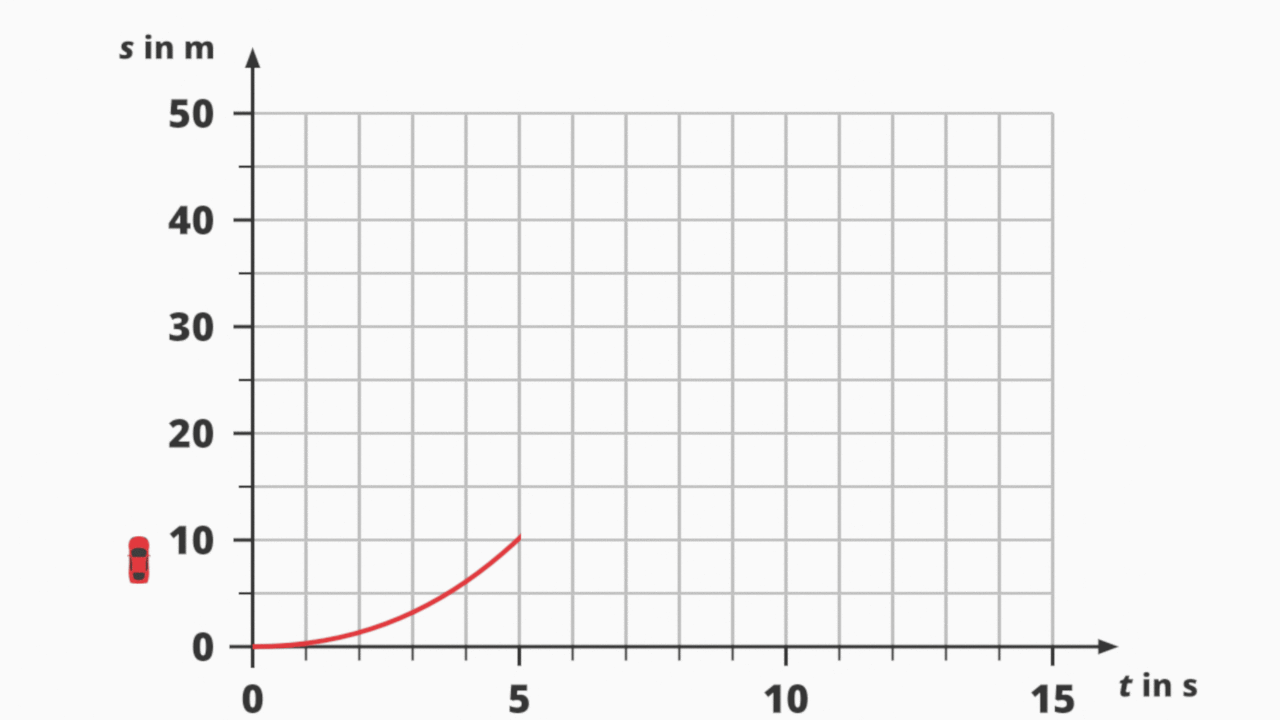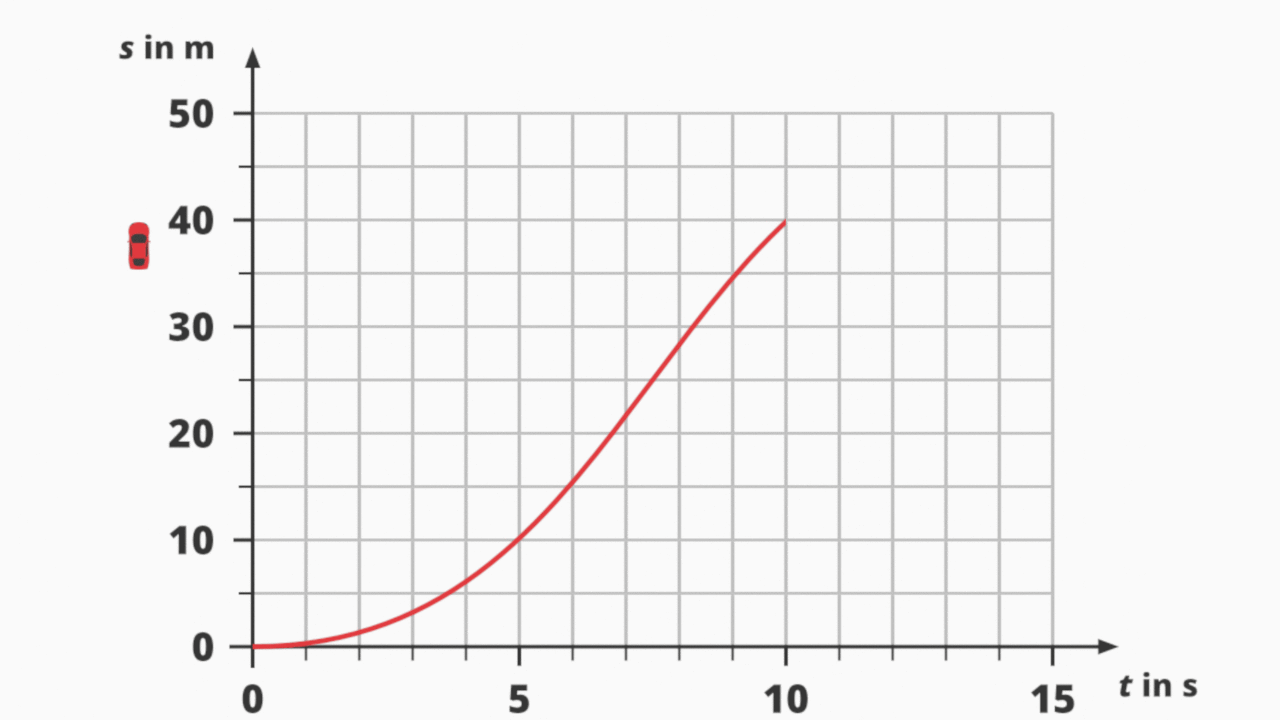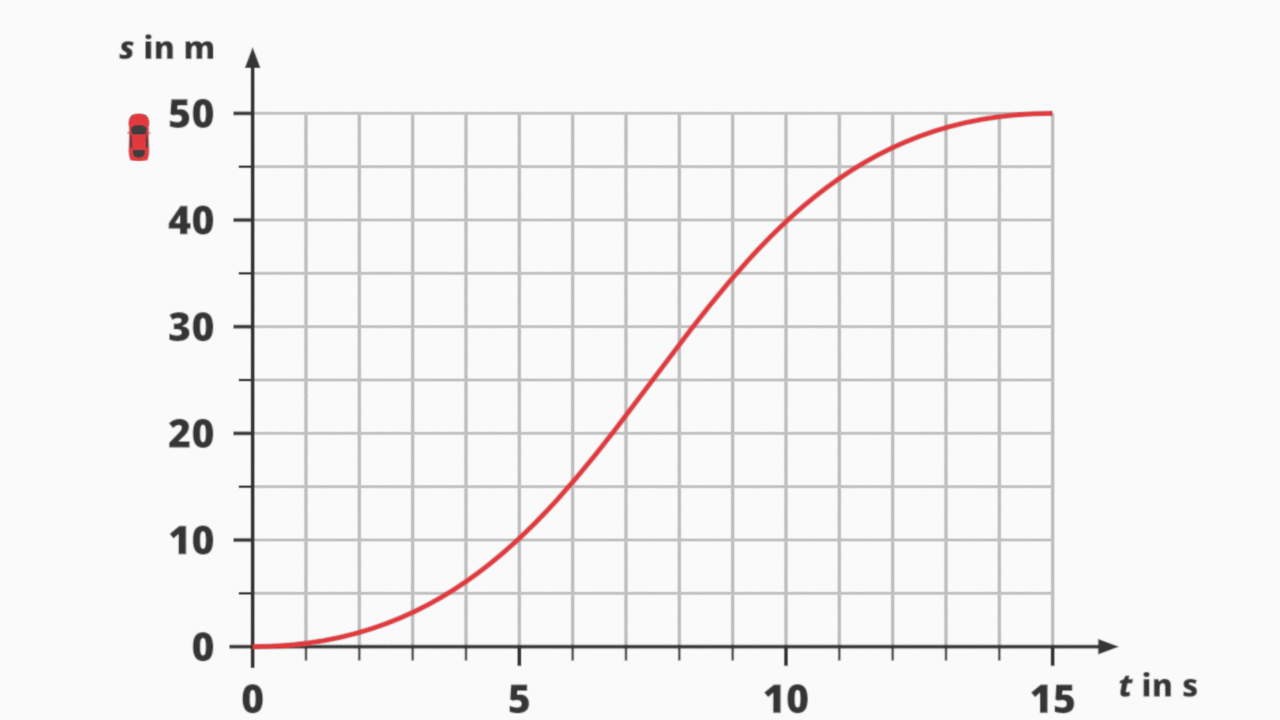
s(t)-Diagramm einer ungleichförmigen Bewegung.
In der Animation siehst du ein Auto, das beschleunigt und anschließend bremst sowie das zugehörige s(t)-Diagramm. Der Anstieg des Graphen ist jede Sekunde unterschiedlich. Der Weg s und die Zeit t sind somit nicht proportional. (Achtung: „Nicht proportional“ und „antiproportional“ sind nicht dasselbe!)
Eine Bewegung gilt also als ungleichförmig, wenn ein Körper nicht in denselben Zeitabständen denselben Weg zurücklegt.
Aufgabe A – Ungleichförmige Bewegungen beschreiben
Schau dir noch einmal die Animation an. Beschreibe die Bewegung des Autos in Worten.
Aufgabe B – Gleichförmig oder ungleichförmig?
Sind die folgenden Bewegungen gleichförmig oder ungleichförmig? Wähle die jeweils richtige Antwort aus.
Aufgabe C – Ungleichförmige Bewegungen beurteilen
In folgendem Quiz siehst du s(t)-Diagramme mit ungleichförmigen Bewegungen. Kreuze die richtigen Aussagen an. Es können auch mehrere Aussagen richtig sein.
2.3 Durchschnittsgeschwindigkeit
Im letzten Kapitel hast du gelernt, wie du die Geschwindigkeit von gleichförmigen Bewegungen berechnen kannst. Bei ungleichförmigen Bewegungen ist das nicht ganz so einfach, da sich der Anstieg des Graphen im s(t)-Diagramm stets verändert.
Um die „Schnelligkeit“ einer ungleichförmigen Bewegung beschreiben zu können, kannst du die sogenannte Durchschnittsgeschwindigkeit (auch mittlere Geschwindigkeit genannt) berechnen. Dabei wird der Anstieg in einem größeren Zeitraum betrachtet.
§
Urheber: Digitale Lernwelten GmbH
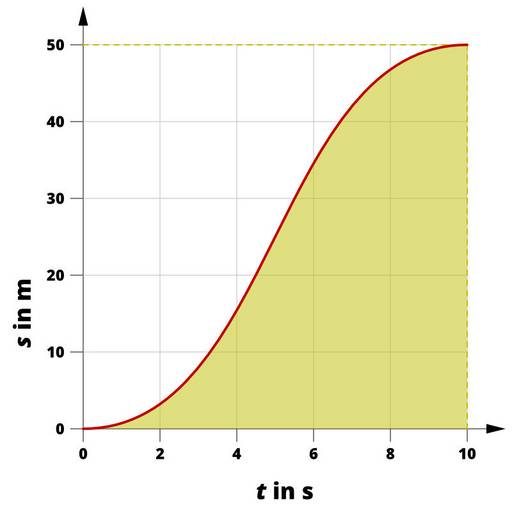
Für die Berechnung der Durchschnittsgeschwindigkeit wird ein größerer Zeitraum betrachtet.
In nebenstehendem s(t)-Diagramm hat der Körper nach 10 Sekunden einen Weg von 50 Metern zurückgelegt.
v = s / t
v = 50 m / 10 s
v = 5 m/s
Die Durchschnittsgeschwindigkeit des Körpers beträgt 5 m/s. Die Formel gleicht der Berechnung der Geschwindigkeit bei gleichförmigen Bewegungen. Im Falle einer gleichförmigen Bewegung entspricht die Durchschnittsgeschwindigkeit eines Körpers immer seiner Geschwindigkeit (da er zu jedem Zeitpunkt gleich schnell ist).
§
Urheber: Digitale Lernwelten GmbH
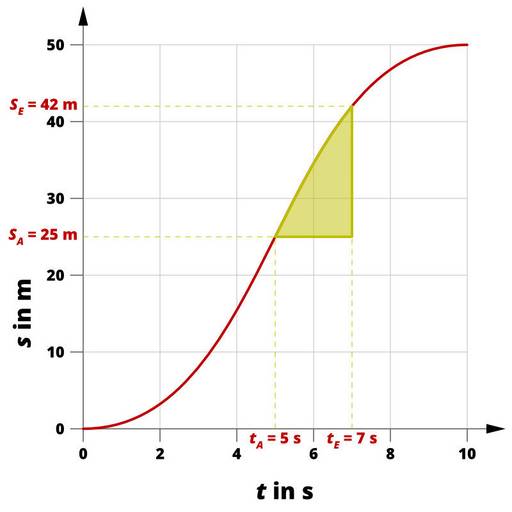
Berechnung der Durchschnittsgeschwindigkeit für einen bestimmten Zeitraum.
Die Durchschnittsgeschwindigkeit kann auch für einen ausgewählten Zeitraum berechnet werden. Dafür wird zunächst der Anfangs- und Endzeitpunkt bestimmt (in diesem Fall bei 5 und 7 Sekunden):
t = tE - tA
t = 7 s - 5 s
t = 2 s
Der Zeitraum (t) beträgt 2 s. An den Anfangs- und Endzeitpunkten kann abgelesen werden, welchen Weg der Körper in diesem Zeitraum zurücklegt:
s = sE - sA
s = 42 m - 25 m
s = 17 m
Der Weg (s) beträgt 17 m. Nun werden die Werte in die Formel eingesetzt:
v = s / t
v = 17 m / 2 s
v = 8,5 m/s
Die Durchschnittsgeschwindigkeit des Körpers (v) beträgt in dem ausgewählten Zeitraum 8,5 m/s. Schau dir noch einmal das s(t)-Diagramm an und verfolge die einzelnen Rechenschritte im Diagramm.
Aufgabe – Durchschnittsgeschwindigkeit berechnen
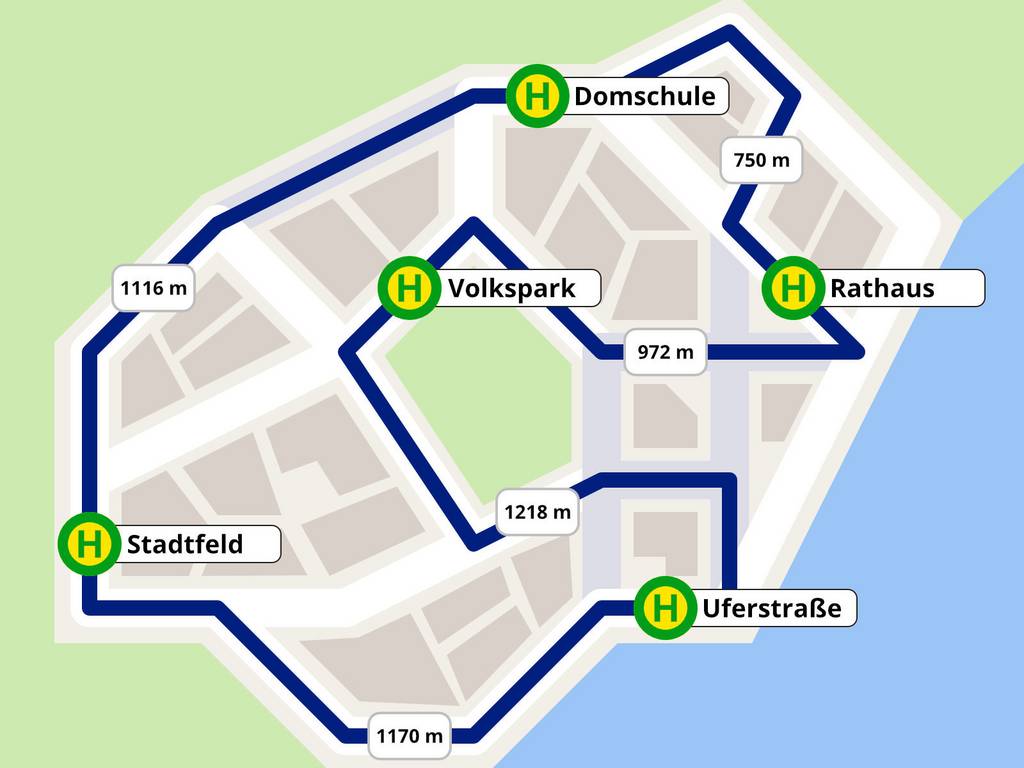
Auf der Karte ist die Route einer Buslinie eingezeichnet. Du siehst die Positionen der Haltestellen sowie die Entfernungen zwischen den Haltestellen. Darunter befindet sich der Fahrplan der Buslinie.
Berechne die Durchschnittsgeschwindigkeit des Busses in den jeweiligen Abschnitten. In welchem Abschnitt erreicht der Bus die höchste Durchschnittsgeschwindigkeit?
§
Urheber: Digitale Lernwelten GmbH
Der Bus startet an der Haltestelle „Stadtfeld“. Er hält im Uhrzeigersinn an den Haltestellen „Domschule“, „Rathaus“, „Volkspark“ und „Uferstraße“ und endet wieder an der Haltestelle „Stadtfeld“.
| Haltestelle | Uhrzeit (alle 30 min) |
|---|---|
| Stadtfeld | 06:00 |
| Domschule | 06:06 |
| Rathaus | 06:11 |
| Volkspark | 06:17 |
| Uferstraße | 06:24 |
| Stadtfeld | 06:30 |
Methode
Wie wird ein Experiment durchgeführt?
Methode
Wie wird ein Experiment durchgeführt?
Wie wird ein Experiment durchgeführt?
Experimente sind ein wichtiger Teil der Naturwissenschaften. In der naturwissenschaftlichen Forschung werden Hypothesen (Vermutungen) aufgestellt, wie die Welt funktioniert und zusammenhängt. Mithilfe von Experimenten können diese Hypothesen überprüft und neue Erkenntnisse gewonnen werden.
Die Durchführung eines Experiments folgt einem festen Ablauf, damit das Experiment reproduzierbar ist. Das heißt, das Experiment muss immer zu demselben Ergebnis führen, wenn es unter denselben Bedingungen durchgeführt wird.
Das gesamte Experiment – von der Aufgabenstellung bis zur Auswertung – wird in einem Versuchsprotokoll dokumentiert. Das Versuchsprotokoll sollte folgenden Aufbau haben:
Experiment
100-Meter-Sprint: Lauf gegen Fahrrad
Experiment
100-Meter-Sprint: Lauf gegen Fahrrad
100-Meter-Sprint
In diesem Experiment lasst ihr zwei Personen in einem Rennen über 100 Meter gegeneinander antreten. Eine Person läuft, die andere fährt Fahrrad.
Materialien & Personen
- Eine Laufbahn (min. 100 Meter Länge)
- Ein Fahrrad
- 10 Stoppuhren (oder Smartphones)
- Mindestens 12 Personen
Achtung: Wenn ihr weniger als 12 Personen seid oder dieses Experiment zu Hause bearbeitet, überspringt die Durchführung und verwendet die Werte, die in Aufgabe C hinterlegt sind.
Durchführung

§
Urheber: Digitale Lernwelten GmbH
Versuchsaufbau
- Bestimmt, welche Person läuft und welche Fahrrad fährt. Die anderen 10 Personen positionieren sich mit jeweils einer Stoppuhr in gleichmäßigen Abständen an der Laufbahn (die erste Person 10 Meter von der Startlinie entfernt, die zweite zwanzig Meter usw. – die letzte Person sollte 100 Meter von der Startlinie entfernt sein).
- Zuerst positioniert sich der Läufer an der Startlinie. Der Fahrradfahrer übernimmt die Versuchsleitung und protokolliert die Messwerte.
- Sobald die Versuchsleitung „Los!“ ruft, läuft der Läufer los und die 10 Personen mit den Stoppuhren beginnen die Zeitmessung.
- Wenn der Läufer eine Person mit Stoppuhr passiert, hält diese Person die Zeitmessung an. Nachdem der Läufer das Ziel erreicht hat, werden alle gemessenen Zeiten von der Versuchsleitung protokolliert.
- Die Punkte 2-4 werden wiederholt. Doch diesmal wird die Zeit des Radfahrers gemessen und der Läufer übernimmt die Versuchsleitung.
Aufgabe A – Versuchsplanung Lauf gegen Fahrrad
Schau dir zunächst die Aufgabenteile B bis H an, bevor du mit dem Experiment beginnst und überlege dir, welche Aufgaben...
- zur Vorbereitung des Experiments gehören.
- zur Durchführung des Experiments gehören.
- zur Auswertung des Experiments gehören.
Erstelle dir einen Plan, welche Aufgaben du vor, während und nach dem Experiment bearbeitest.
Aufgabe B – Hypothese aufstellen
Stelle zunächst deine Hypothese auf:
- Wer benötigt weniger Zeit, um das Ziel zu erreichen?
- Wer erreicht die höhere Geschwindigkeit?
Begründe deine Hypothese.
Aufgabe C – Beobachtungen dokumentieren
Wenn du das Experiment nicht durchführen konntest, nutze die in der Tabelle hinterlegten Werte für die weiteren Aufgaben. Wenn ihr das Experiment durchgeführt habt, tragt die Messwerte in die Tabelle ein.
Nutze das Textfeld, um weitere Beobachtungen zu notieren.
Aufgabe D – Messwerte auswerten
Erstelle ein gemeinsames s(t)-Diagramm für die beiden dokumentierten Bewegungen.
Du kannst ein Foto deines Diagramms hochladen, um dein Ergebnis hier festzuhalten.
Aufgabe E – Durchschnittsgeschwindigkeit berechnen
- Berechne die Durchschnittsgeschwindigkeit für beide Bewegungen über den gesamten Zeitraum.
- In welchem Abschnitt haben die beiden Bewegungen jeweils ihre größte Durchschnittsgeschwindigkeit?
Aufgabe F – Hypothese überprüfen
Überprüfe deine Hypothese und beantworte die folgenden Fragen:
- Wer benötigte weniger Zeit? Wer hat die höhere Geschwindigkeit erreicht? Handelt es sich um dieselbe Person?
- Konnte der Fahrradfahrer den Läufer überholen?
- Wenn ja: Gib den Zeitpunkt an, zu dem der Fahrradfahrer den Läufer überholt.
- Wenn nicht: Warum konnte der Fahrradfahrer den Läufer nicht überholen?
Aufgabe G – Fehlerquellen überprüfen
Welche Faktoren können bei diesem Versuch zu möglichen Ungenauigkeiten oder Abweichungen führen?
Wie können sich diese Faktoren auf die dokumentierten Zeiten auswirken?
Aufgabe H – 200-Meter-Sprint
Wie würde das s(t)-Diagramm aussehen, wenn ihr den Versuch über eine Distanz von 200 Metern wiederholt? Gib eine Vermutung aufgrund der bisherigen Erkenntnisse ab.
2.4 Zusatzmodul: Mit bloßem Auge ...
Manche Bewegungen sind so schnell, dass du sie mit bloßem Auge nicht erkennen kannst. Andere Bewegungen sind so langsam, dass du sie selbst mit ganz viel Geduld nicht beobachten kannst. Schau dir die folgenden Bilder an:

§
Urheber: Alexandre Bringer
https://www.pexels.com/de-de/foto/blitz-unk-auf-grunem-grasfeld-3637060/
Blitze tasten sich vor, bis sie Kontakt zum Boden haben.

§
Urheber: Pixabay
https://www.pexels.com/de-de/foto/wassertropfen-40784/
Ein Wassertropfen trifft auf eine Wasseroberfläche.

§
Urheber: Aviv Perets
https://www.pexels.com/de-de/foto/berg-und-himmel-3274903/
Eine Langzeitbelichtung zeigt die Bewegung des Sternenhimmels.

§
Urheber: Jen Theodore
https://unsplash.com/photos/Tys0QOcdbBA
Ein Samen keimt und wächst über mehrere Tage zu einer Pflanze heran.
Bei einem Gewitter ist häufig zuerst der Blitz zu sehen und das Geräusch des Donners folgt etwas später. Grund dafür ist, dass sich Licht und Schall mit unterschiedlichen Geschwindigkeiten ausbreiten.
Licht bewegt sich mit einer Geschwindigkeit von ungefähr 300.000 Kilometern pro Sekunde. Damit ein Zeitunterschied wahrgenommen werden kann, muss die Distanz zwischen der Lichtquelle und dem Auge sehr groß sein.
Schall bewegt sich dagegen „nur“ mit einer Geschwindigkeit von ungefähr 343 m/s. Deshalb hörst du das Geräusch eines Blitzes erst, nachdem du ihn siehst.
Wenn du den zeitlichen Abstand zwischen Blitz und Donner misst, kannst du anhand der Schallgeschwindigkeit berechnen, wie weit der Blitz entfernt ist:
s = v * t
s = Schallgeschwindigkeit * zeitlicher Abstand in Sekunden
Aufgabe A – Schallgeschwindigkeit
Du siehst einen Blitz und hörst anschließend den Donner. Der zeitliche Abstand zwischen Blitz und Donner beträgt 5 Sekunden. Berechne die Entfernung zwischen dir und dem Blitz.
Aufgabe B – Lichtgeschwindigkeit
Der Abstand zwischen der Sonne und der Erde beträgt ungefähr 150 Millionen Kilometer. Berechne die Zeit, die das Sonnenlicht benötigt, um zur Erde zu gelangen.
Erweiterung: das Voyager-Programm

§
Urheber: NASA/JPL
https://commons.wikimedia.org/wiki/File:Voyager_spacecraft.jpg
Darstellung der Voyager-Sonde im All
Das Voyager-Programm ist ein Forschungsprogramm der NASA zur Erkundung der äußeren Planeten unseres Sonnensystems und des interstellaren Raums (Raum außerhalb des Sonnensystems).
Teil des Programms war der Start der beiden Raumsonden Voyager 1 und Voyager 2 im Jahr 1977. Beide Missionen dauern bis heute an.
Beide Raumsonden passierten mehrere Planeten unseres Sonnensystems und befinden sich mittlerweile im interstellaren Raum. Voyager 1 ist das am weitesten von der Erde entfernte Objekt, das von Menschen geschaffen wurde und sendet noch immer Signale zur Erde. Es befindet sich aktuell (Stand: März 2021) ca. 22,8 Milliarden Kilometer von der Sonne entfernt.
Aufgabe A - Die Reise der Voyager 2
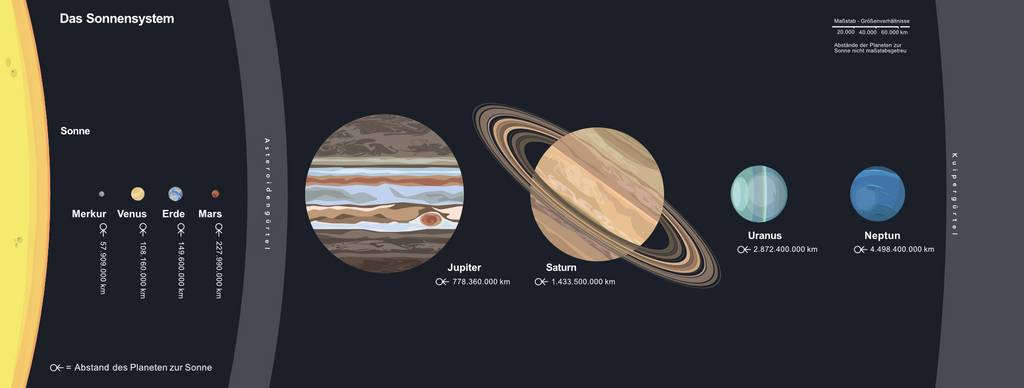
Die folgende Tabelle zeigt den zeitlichen Verlauf der Voyager 2-Mission. Darunter befindet sich eine Grafik mit den Entfernungen der Planeten zur Sonne. Stelle die Bewegung der Raumsonde in einem s(t)-Diagramm dar. Achte dabei vor allem auf eine passende Achseneinteilung.
Nimm für die Darstellung im Diagramm vorerst an, dass sich die Raumsonde in den jeweiligen Zeitabschnitten gleichförmig bewegt und sich die Planeten in einer geraden Linie befinden.
| Datum | Ereignis |
|---|---|
| 20.08.1977 | Start auf der Erde |
| 09.07.1979 | Vorbeiflug am Jupiter |
| 26.08.1981 | Vorbeiflug am Saturn |
| 24.01.1986 | Vorbeiflug am Uranus |
| 25.08.1989 | Vorbeiflug am Neptun |
§
Urheber: Original von Beinahegut (bearbeitet von Digitale Lernwelten)
https://commons.wikimedia.org/wiki/File:Sonnensystem-Grafik.pdf
Aufgabe B - Geschwindigkeit der Voyager 2
Berechne die Durchschnittsgeschwindigkeit von Voyager 2 für die jeweiligen Zeitabschnitte.
- In welchem Abschnitt ist die Durchschnittsgeschwindigkeit am größten?
- Äußere eine Vermutung, warum sich die Geschwindigkeit von Voyager 2 verändert.
Aufgabe C - Flugbahnen der Voyager-Sonden
Rechts siehst du ein Bild der Flugbahnen der Voyager-Sonden.
- Beschreibe die Flugbahnen. Was fällt dir auf?
- Worauf mussten die Wissenschaftler achten als sie das Startdatum der Sonden gewählt haben?
Zusammenfassung
Bewegungsformen
Zusammenfassung
Bewegungsformen
1. Bahnformen
Die Bahnform bezeichnet die Bahn, entlang der sich ein Körper bewegt. Folgende Bahnformen hast du in diesem Kapitel kennengelernt:
- Geradlinige Bewegung: Der Körper bewegt sich entlang einer Geraden.
- Kreisbewegung: Der Körper bewegt sich auf einer kreisförmigen Bahn.
- Schwingung: Der Körper bewegt sich zwischen zwei Punkten hin und her.
2. Ungleichförmige Bewegungen
Eine Bewegung ist ungleichförmig, wenn der Körper nicht in denselben Zeitabständen denselben Weg zurücklegt. Der Graph einer ungleichförmigen Bewegung ist keine Gerade, s und t verhalten sich nicht proportional zueinander.
In der Natur bewegen sich nahezu alle Körper ungleichförmig, da sie zuerst einmal beschleunigen und irgendwann wieder abbremsen müssen.
3. Durchschnittsgeschwindigkeit
§
Urheber: Digitale Lernwelten GmbH
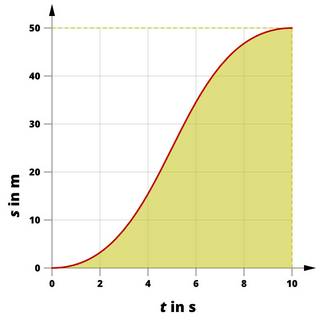
Bestimmung der Durchschnittsgeschwindigkeit bei einer ungleichförmigen Bewegung.
Um die „Schnelligkeit“ einer ungleichförmigen Bewegung zu beschreiben, kann die Durchschnittsgeschwindigkeit berechnet werden. Dabei wird der Anstieg in einem größeren Zeitraum betrachtet:
v = s / t
v = 50 m / 10 s
v = 5 m/s
Der Körper bewegt sich mit einer Durchschnittsgeschwindigkeit von 5 m/s.
§
Urheber: Digitale Lernwelten GmbH
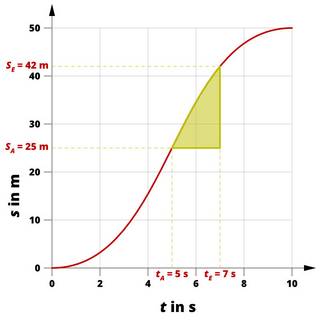
Die Durchschnittsgeschwindigkeit kann auch für ausgewählte Zeiträume bestimmt werden.
Die Durchschnittsgeschwindigkeit kann auch für beliebige Zeiträume bestimmt werden:
v = s / t = (sE - sA) / (tE - tA)
v = (42 m - 25 m) / (7 s - 5 s) = 17 m / 2 s
v = 8,5 m/s
Der Körper bewegt sich im angegebenen Zeitraum mit einer Durchschnittsgeschwindigkeit von 8,5 m/s.
4. Durchführung eines Experiments
Experimente sind ein wichtiger Teil der Naturwissenschaften. Sie werden in einem Versuchsprotokoll dokumentiert, das folgenden Aufbau haben sollte:
- Name des Protokollanten
- Thema bzw. Fragestellung
- Hypothese
- Geräte und Materialien
- Versuchsaufbau
- Durchführung
- Beobachtung
- Auswertung
5. Entfernungen und Geschwindigkeiten in der Astronomie
Auch Schall und Licht breiten sich mit einer Geschwindigkeit aus.
- Die Schallgeschwindigkeit beträgt ungefähr 343 m/s.
- Die Lichtgeschwindigkeit beträgt ungefähr 300.000 km/s.
Die Distanz zwischen der Erde und der Sonne beträgt ungefähr 150 Millionen Kilometer.