Ein Quadrat hat die besondere Eigenschaft, dass seine Seiten alle gleich lang sind. Außerdem hat es vier rechte Winkel.

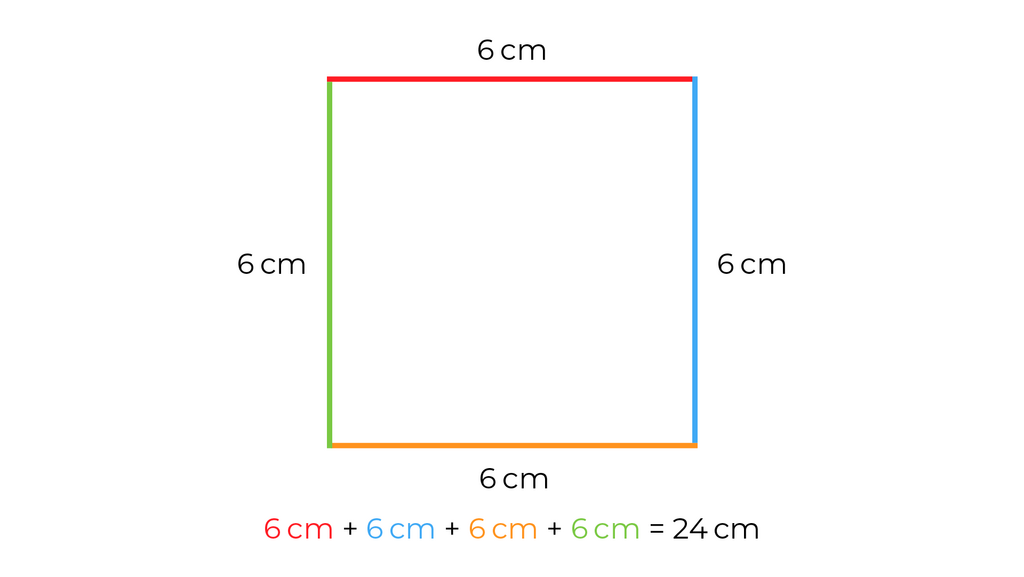
Wenn du alle vier Seiten des Quadrats addierst,  berechnest du den Umfang. 

Wenn man einmal um das Quadrat herumgehen würde, wäre der Umfang die zurückgelegte Strecke.

Jetzt lernst du eine neue Figur kennen, den Kreis. Auch ein Kreis hat einen Umfang.

Genau wie beim Quadrat ist auch hier der Umfang die Strecke, die man zurücklegt, wenn man einmal um den Kreis herum läuft.

Nimm dir einen Zirkel und zeichne einen Kreis.

Die Bleistiftlinie, die entstanden ist, ist auch der Umfang deines Kreises.

Wenn uns seine Länge nicht interessiert, kann man diese Linie auch Kreislinie nennen.

Betrachte dein Blatt. Ist außer der Linie noch etwas zu erkennen?

Deutlich zu sehen ist auch die Stelle, an welcher du den Zirkel in das Papier gestochen hast.

Sie liegt genau in der Mitte deines Kreises. Deshalb nennen wir sie Mittelpunkt.

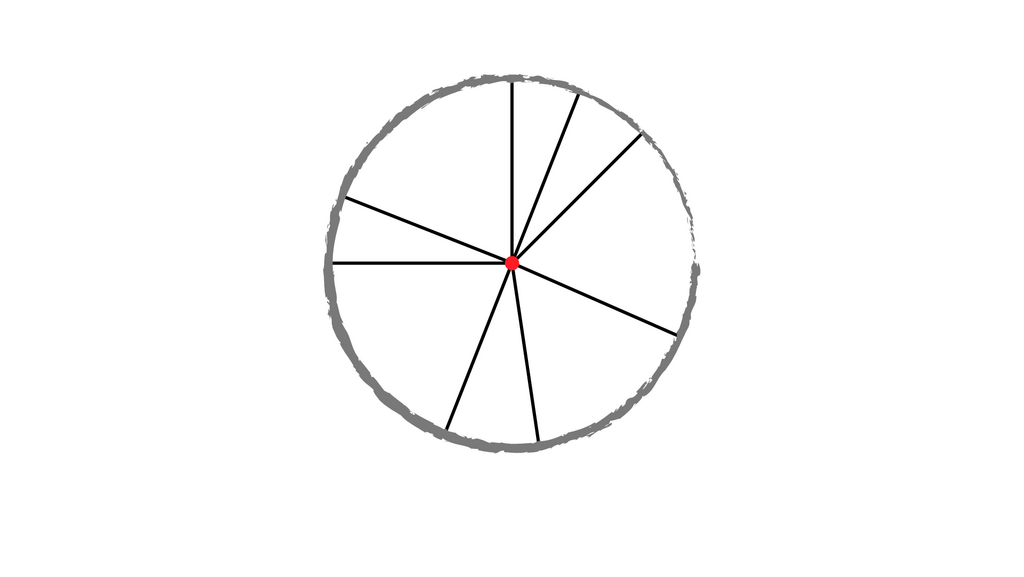
Nimm dir nun dein Geodreieck und zeichne an verschiedenen Stellen eine Linie vom Mittelpunkt zur Kreislinie. Fällt dir etwas auf?

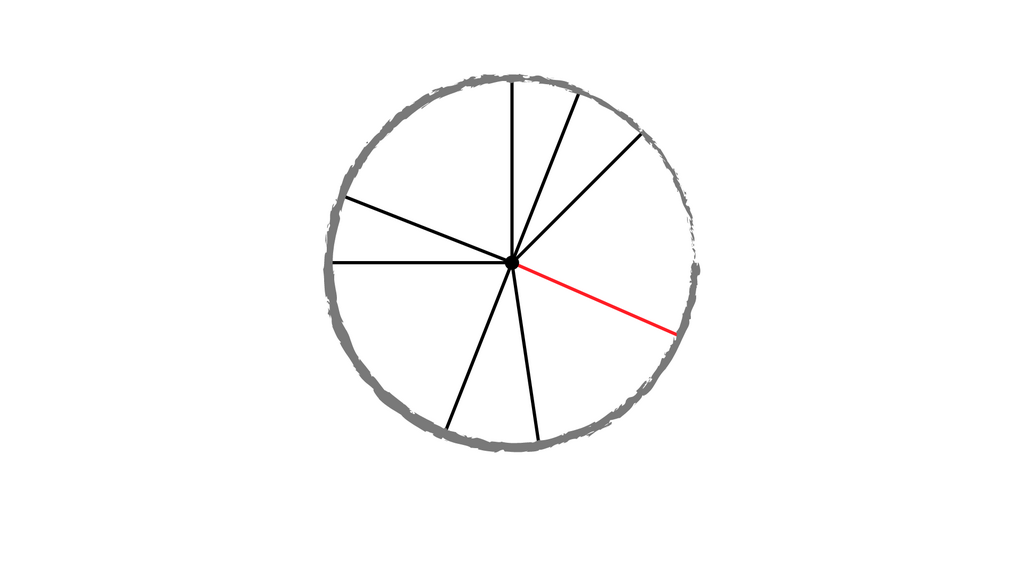
Dir ist vielleicht aufgefallen, dass alle die Linien gleich lang sind. Deshalb haben sie einen besonderen Namen.

Eine Linie vom Mittelpunkt zum Kreisring nennt man Radius. 

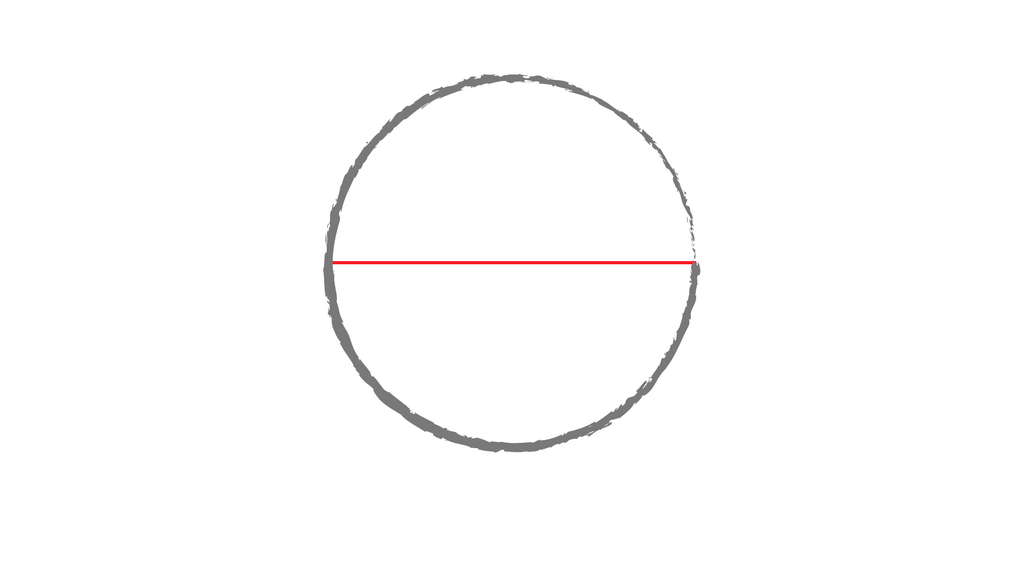
Zeichne nun eine Line, die von einer Seite der Kreislinie zur anderen und dabei durch den Mittelpunkt geht.

Diese Linie nennt man Durchmesser. 

Hat diese neue Linie etwas mit dem Radius zu tun? Teste, indem du die Punkte in der Grafik verschiebst.

Hast du es entdeckt? Diese Linie ist zweimal so lang wie der Radius.

Um dich an etwas Anderes zu erinnern: Zeichne ein Quadrat und male es in einer bunten Farbe aus.

Auch ein Kreis hat solch einen Flächeninhalt.

Zeichne einen neuen Kreis und male alles innerhalb der Kreislinie bunt an.

Alles, was nun bunt gemalt ist, ist der Flächeninhalt eines Kreises.

Was musst du dir merken?

Ein Kreis entsteht, wenn wir eine Kreislinie zeichnen. Wenn uns die Länge dieser Linie interessiert, nennen wir sie auch Umfang (abgekürzt ‚u‘).

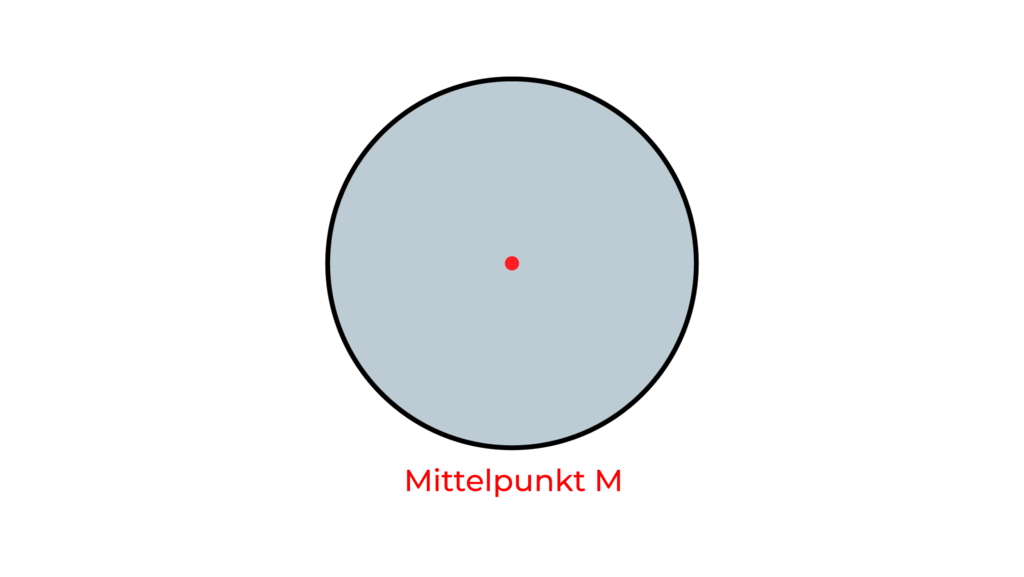
In der Mitte hat jeder Kreis seinen Mittelpunkt.

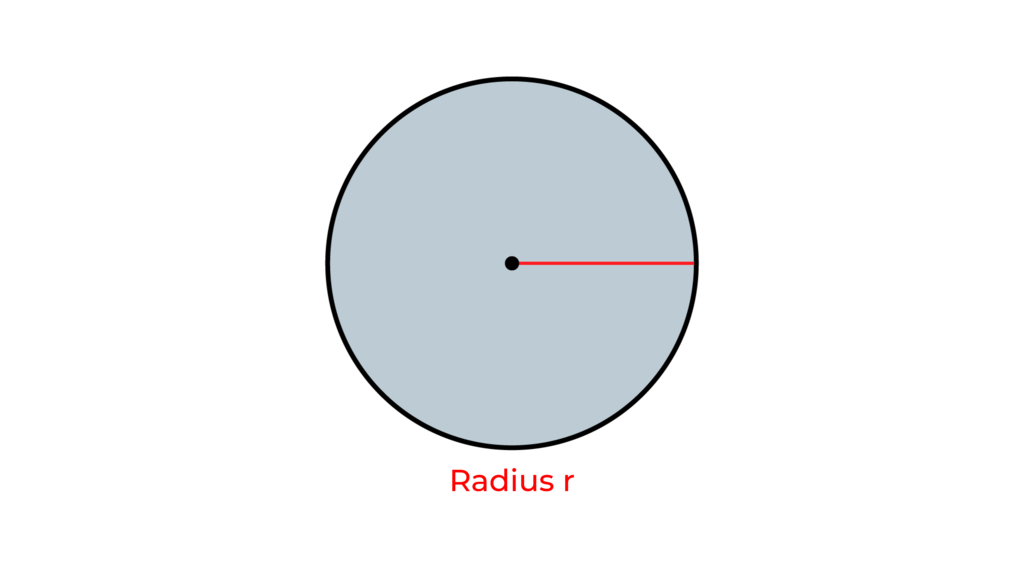
Die Linie vom Mittelpunkt zur Kreislinie nennt man Radius (abgekürzt ‚r‘). 

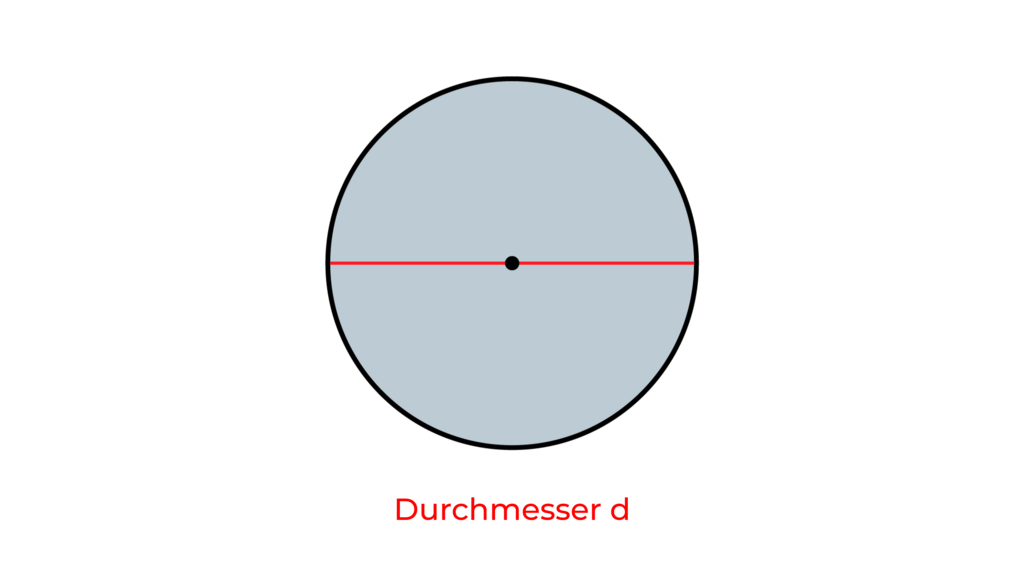
Eine Linie, die die Kreislinie zweimal und einmal den Mittelpunkt berührt, nennt man Durchmesser (abgekürzt ‚d‘). Sie ist zweimal so lang wie der Radius.

Alles, was innerhalb der Kreislinie liegt, ist der Flächeninhalt (abgekürzt ‚A‘) des Kreises.

Du hast es geschafft! Versuche nun die Aufgaben im Kapitel zu lösen.