3 Der Kathetensatz

Urheber: Digitale Lernwelten GmbH

Aufgabe 1

Zeichne drei unterschiedliche, rechtwinklige Dreiecke. Zeichne die Höhe h_csowie q und p ein.

Merke

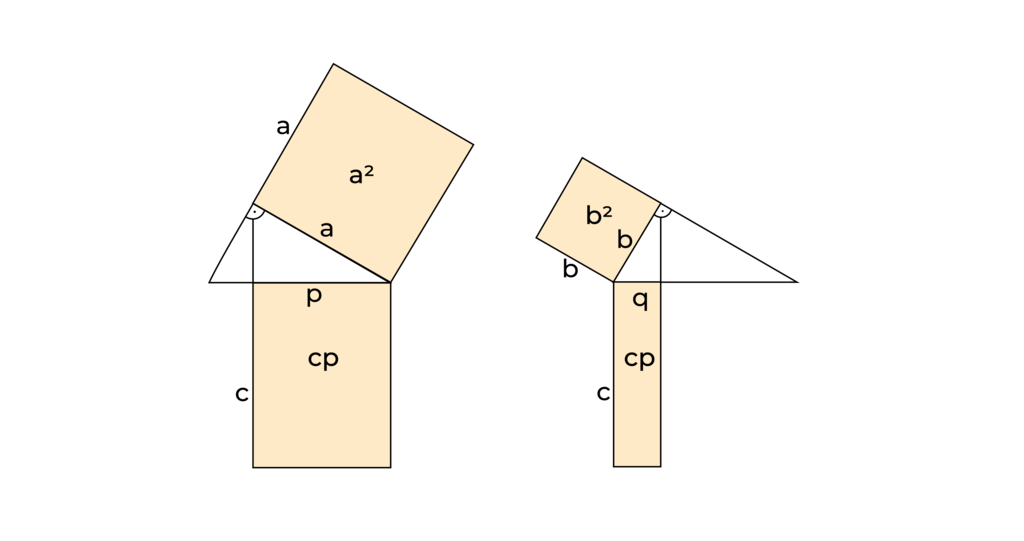
Wenn ein Dreieck einen rechten Winkel hat, dann ist das Quadrat einer Kathete flächengleich zum Rechteck aus der Hypotenuse und dem Hypotenusenabschnitt.

Aufgabe 2

Konstruiere die folgenden Quadrate:

a.) 14 cm²

b.) 22 cm²

c.) 29 cm²

Umkehrung des Kathetensatzes

Merke:

Gegeben sei ein Dreieck ABC mit Seiten a, b und c, wobei c die Hypotenuse sei. Die Höhe auf die Seite c teilt diese in zwei Abschnitte q und p, wobei der Abschnitt p an der Seite a, der Abschnitt q an der Seite b anliegt.
Wenn nun die Beziehungen

gelten, dann ist das Dreieck ABC rechtwinklig.

Aufgabe

Gegeben sind das Quadrat mit a² und die Länge p. Wie groß muss c sein, damit die Umkehrung des Kathetensatzes gilt? Berechne anschließend die Länge der Kathete a.

a.) 42,8 cm² = c * 4,81 cm

b.) 9,71 cm² = c * 1,5 cm

c.) 30,21 cm² = c * 2,65 cm