Dass wir den Kreis und seine Größen heute problemlos berechnen können, ist kein Zufall. Bereits vor über 1000 Jahren versuchten schlaue Köpfe, die Geheimnisse des Kreises zu lösen. Genaueres erfährst du im Video im Ausschnitt 02:26 - 06:10.

§
Urheber: geralt
Pixabay
2.1 Die Suche nach der Kreiszahl

§
Zusatz: Interessiert es dich, wie Archimedes ganz ohne Computer und Taschenrechner π bestimmt hat?
Zusatz: Interessiert es dich, wie Archimedes ganz ohne Computer und Taschenrechner π bestimmt hat?

§
Urheber: Digitale Lernwelten GmbH
Klicke auf die zwei fehlenden Kästchen im GeoGebra-Fenster. In allen vier muss ein Häkchen sein. Ziehe dann an den Schiebereglern.
§
CC BY-SA 3.0
Urheber: Camylle Buck
2.2 Die Kreiszahl und der Umfang des Kreises
Zur Berechnung des Kreisumfangs brauchen wir die Kreiszahl π. Aber wie kommt man auf die komplette Formel?
Bewege den Kreis im GeoGebra-Fenster, indem du am blauen Punkt ziehst und stelle eine Vermutung auf.
§
CC BY-SA 3.0
Urheber: mnerlich
Förderfenster: Wie funktioniert eine mathematische Formel?
Den Kreisumfang berechnet man mit dieser Formel:
u = π * d
Buchstaben können Mathe noch schwerer aussehen lassen.
Keine Angst vor Buchstaben! Ich helfe dir.
§
Urheber: Digitale Lernwelten GmbH
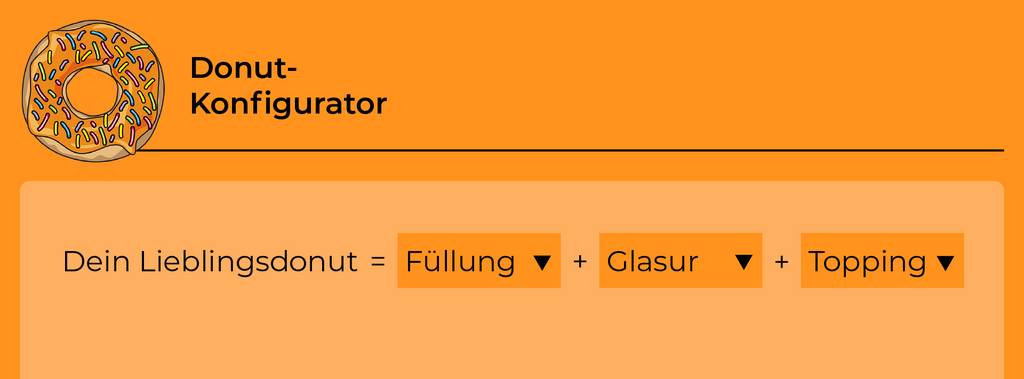
Lass es mich mithilfe eines Donuts erklären:
Manche Donutshops bieten an, sich online den persönlichen Lieblingsdonut zusammenzustellen. Das sieht dann ungefähr so aus.

§
Urheber: Digitale Lernwelten GmbH
Um deinen Lieblingsdonut zu erstellen, musst du dir nur deine Lieblingsgeschmäcker raussuchen.
Wie würde dein Lieblingsdonut aussehen? Schreibe auf.
Der Konfigurator gibt dir genau vor, welche Bestandteile deines Donuts du gestalten kannst. Das erkennst du an den Worten. In diesem Fall:
Füllung, Glasur und Topping.

§
Urheber: Digitale Lernwelten GmbH
An der Stelle, an der die Wörter Füllung, Glasur und Topping stehen, musst du deine Lieblingsgeschmäcker einsetzen.
Damit gibst du dem Bäcker eine Bauanleitung für deinen Donut.
Du könntest es auch als Text schreiben, das wäre aber viel unübersichtlicher.
Mit der Bauanleitung sieht der Bäcker viel schneller, was er machen muss.

§
Urheber: Digitale Lernwelten GmbH
Eine mathematische Formel funktioniert wie ein Donutkonfigurator.
-> Achtung! Es wird mathematisch.
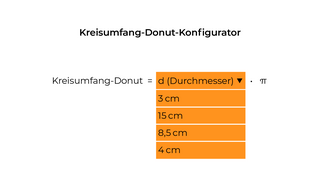
Nehmen wir an, der Umfang eines Kreises wäre ein Donut.
Der Umfang wird gesucht.
Der Konfigurator würde uns Folgendes vorgeben:
§
Urheber: Digitale Lernwelten GmbH
Die Formel sagt dir: Dort, wo d (Durchmesser) steht, musst du die Größe des Durchmessers einsetzen.
Diese erfährst du in der Aufgabenstellung.
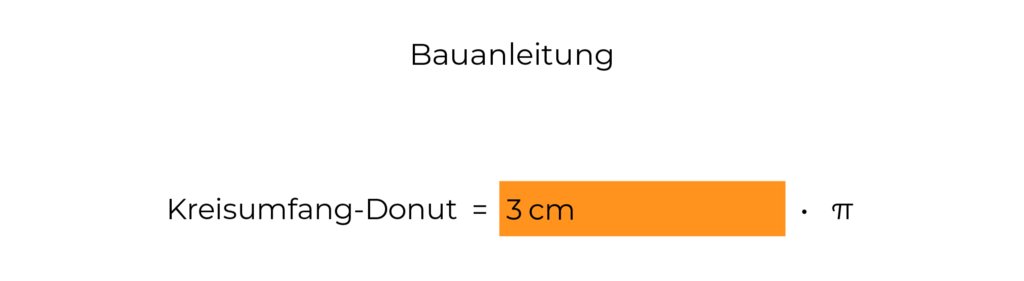
Aufgabe:
Der Durchmesser des Kreises ist 3 cm.
Gegeben ist in diesem Fall: d = 3 cm.
π kann man nicht verändern, es gehört immer dazu.
Jetzt bist du dran. Notiere dir die Formel und die Rechnung.
§
Urheber: Digitale Lernwelten GmbH
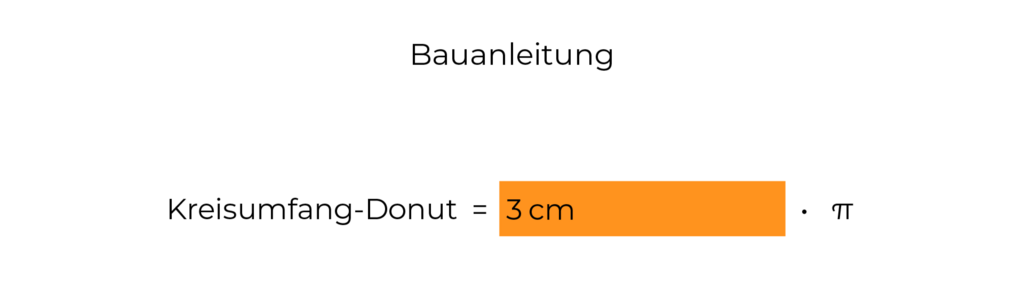
Die Bauanleitung für unseren Kreisumfang-Donut würde dann so aussehen. Hast du das auch?
§
Urheber: Digitale Lernwelten GmbH
Um den Umfang eines Kreises zu berechnen, musst du zunächst seinen Durchmesser kennen. In dieser Aufgabe ist der Durchmesser des Kreises gleich 3 cm. Nun müssen wir nur noch 3 cm mit der Kreiszahl π multiplizieren, dann erhältst du den Umfang.
Du siehst: Eine Formel ist als Bauanleitung praktischer als der Text. Man kann sie schneller lesen.

§
Urheber: Digitale Lernwelten GmbH
Wenn du dich nun in die Rolle des Bäckers hineinversetzt, musst du nur noch der Anleitung folgen, um diesen Donut zu bauen.
Rechnung:

§
Urheber: Digitale Lernwelten GmbH
Anders gesagt:
Gesucht: Umfang des Kreises u
gegeben: d = 3 cm
Jetzt bist du dran! Berechne und denke an den Antwortsatz.

§
Urheber: Digitale Lernwelten GmbH
Vergleiche deine Lösung.
Ein Kreis hat einen Durchmesser von 4 cm. Wie groß ist sein Umfang? Berechne.
Notiere dir: gesucht, gegeben, Formel, Rechnung und Antwortsatz.

§
Urheber: Digitale Lernwelten GmbH
Vergleiche deine Lösung.
Was solltest du dir merken?
Eine Formel sagt dir, an welcher Stelle du welche Zahl einsetzen musst, um eine andere Zahl zu berechnen.
Formel zur Berechnung des Umfangs eines Kreises
Formel zur Berechnung des Umfangs eines Kreises
u = d * π
oder
u = 2 * r * π
d = Durchmesser; r = Radius
Jetzt bist du dran. Ziehe die Elemente in die Kästchen, um die Gleichung aufzustellen.
Aufgabe
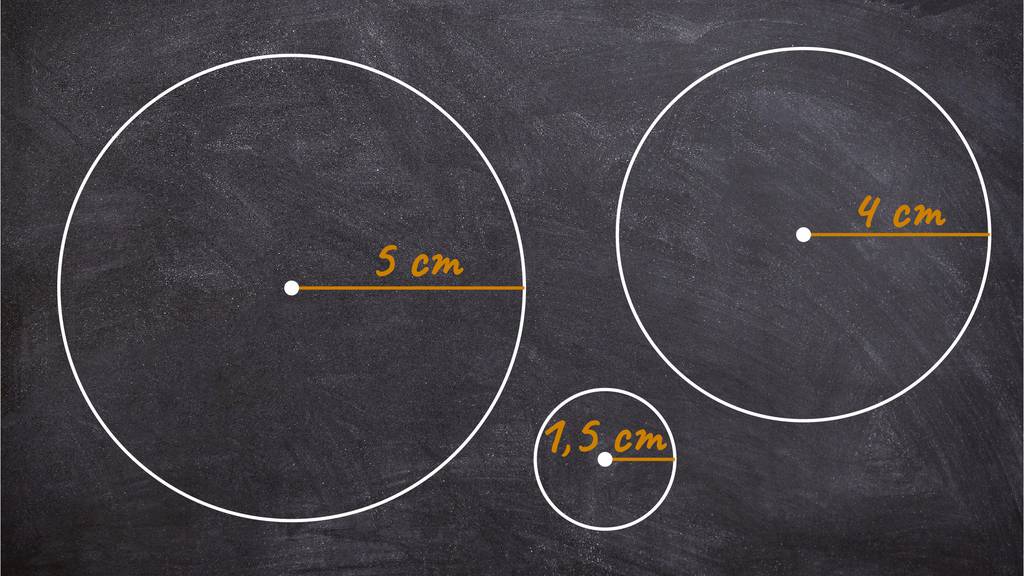
§
Urheber: Digitale Lernwelten GmbH
Berechne den Umfang der Kreise.
2.3 Sinnvolles Runden
Richtig runden
Bearbeite die folgenden Aufgaben.
Schiebe den Regler anschließend nach rechts, um dir die ausführliche Lösung anzusehen.
π sinnvoll runden
π sinnvoll runden
π ist eine unendlich lange Zahl.
Meistens wird sie jedoch auf zwei Nachkommastellen gerundet. Du kannst im Folgenden also mit π ≈ 3,14 rechnen.
Förderfenster: Wie arbeite ich mit Textaufgaben?
Textaufgaben sind bei Schülern unbeliebt.

§
Urheber: Digitale Lernwelten GmbH
Was wird mit diesem Rezept gebacken?
Erstelle eine Zutatenliste!
Versuche aus diesem Text eine Zutatenliste für das Rezept zu erstellen.
Lösung:

§
Urheber: Digitale Lernwelten GmbH
Hast du alle Zutaten herausgelesen?
Was hat das mit Textaufgaben zu tun?
Sehr viel.
Eine Textaufgabe funktioniert wie ein Rezept…

§
Urheber: Digitale Lernwelten GmbH
Der Gärtner legt ein rundes Blumenbeet an. Der Durchmesser beträgt 2,5 m.
Er steckt den Umfang mit einer Schnur ab.
Berechne den Umfang des Beetes! Wie lang ist die Schnur?
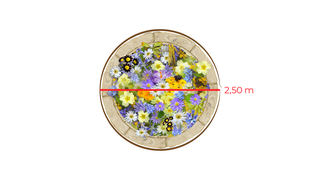
§
Urheber: Digitale Lernwelten GmbH
Du weißt, was gegeben und was gesucht ist.
Jetzt frage dich: Welche Formel benutze ich für diese Berechnung?
Stelle nun die Rechnung auf. Wie funktioniert das? (AUDIOAUFNAHME FEHLT)
Ganz einfach: Wie ein Rezept zeigt dir die Formel die Zutaten, die du brauchst.
u = π * d
π ist immer 3,14.
Die zweite Zutat für unseren Umfang ist der Durchmesser.
Der ist mit 2,5 m gegeben.
Gegeben: Durchmesser d = 2,5 m
Gesucht: Umfang u
Formel: u = π * d
Rechnung: u = 3,14 * 2,5 m
Antwortsatz:
Berechne mit dem Taschenrechner.
Gegeben: Durchmesser d = 2,5 m
Gesucht: Umfang u
Formel: u = π * d
Rechnung: u = 3,14 * 2,5 m
u = 7,85 m
Antwortsatz:
Wie schreibt man den Antwortsatz?
Textaufgaben enden meist mit einer Frage oder einer Aufforderung.
In diesem Beispiel war die Aufforderung:
Berechne den Umfang des Beetes!
Und die Frage:
Wie lang ist die Schnur?
Die Frage kannst du jetzt beantworten.
Antwortsatz: „Die Länge der Schnur beträgt 7,85 m.“ oder „Die Schnur muss 7,85 m lang sein.“
Folgendes Vorgehen kannst du dir bei Textaufgaben merken:
- Welche wichtigen Informationen sind gegeben?
- Was ist gesucht?
- Wie kannst du es berechnen? Notiere die Formel!
- Fülle die Formel …
- Berechne!
- Schreibe den Antwortsatz!
Jetzt bist du dran:
Ein runder Pool soll gebaut werden. Sein Umfang wird mit einer Schnur abgesteckt. Der Durchmesser beträgt 4 m. Wie lang ist diese Schnur (der Umfang des Pools)?
4. Fülle die Formel … und 5. Berechne!
u = 3,14 * 4 m
u = 12,56 m
6. Schreibe einen Antwortsatz
Antwort: Der Umfang des Pools beträgt 12,56 m. Die Schnur ist daher 12,56 m lang.
Jetzt du ganz allein:
Ein Kochtopf hat einen Durchmesser von 20 cm. Wie groß ist sein Umfang?
Gegeben: d = 20 cm
Gesucht: Umfang des Kochtopfes
Formel: u = π *d
Rechnung: u = 3,14 * 20 cm
u = 62,8 cm
Antwortsatz: Der Umfang des Topfes beträgt 62,8 cm (AUDIO)
Aufgabe

§
Pixabay
Um ein rundes Blumenbeet zu pflanzen, muss zunächst der Umfang des Beets mit einer Schnur abgesteckt werden.
Berechne die Länge der Schnur, wenn das Beet:
a.) einen Durchmesser von 2,5 m hat.
b.) einen Durchmesser von 3,3 m hat.
c.) einen Radius von 1,7 m hat.
Runde jeweils auf eine Nachkommastelle.
Aufgabe

§
Urheber: blende12
Pixabay
Der Durchmesser d des Einrads beträgt 20 Zoll (1 Zoll = 2,54 cm).
Welche Strecke legt der Affe zurück, wenn sich das Rad:
a.) einmal komplett dreht?
b.) zweimal komplett dreht?
c.) zehnmal komplett dreht?
Runde auf 2 Nachkommastellen.
Aufgabe

§
Urheber: Sekau67
Pixabay
Das London Eye ist das größte Riesenrad Europas.
Jede Gondel hat eine Entfernung von 61 m zum Mittelpunkt.
Um es nachts zu beleuchten, muss eine Lichterkette um das Rad gesponnen werden. Wie lang ist diese Lichterkette?
Runde auf eine Nachkommastelle.