3. Arten von Zuordnungen

Anmelden
§

Urheber: Shirley810

Pixabay

PD
1

Die Mannschaft des FC Ballpiraten ist wieder unterwegs. Bei ihrem Ausflug braucht sie wieder mathematisches Wissen fĂŒr praktisches Fairplay.

3.1 Zuordnung im Koordinatensystem
2
 ? A B

Aufgabe

Die Mannschaft des FC Ballpiraten besucht nach ihrem letzten Sieg gemeinsam eine Kirmes. Am SĂŒĂŸigkeitenstand kaufen sich alle 11 Mitglieder Leckereien. Jeder erhĂ€lt eine TĂŒte mit 200 g fĂŒr 2,25 €.

  1. Entscheide: Ist diese Zuordnung (SĂŒĂŸigkeiten in g → Preis in €) mehrdeutig, eindeutig oder eineindeutig?
  2. Zeichne ein Koordinatensystem und den Graph A zu dieser Zuordnung.

Als die VerkĂ€uferin am Stand sieht, dass die 11 Mitglieder des FC Ballpiraten alle zusammengehören, sagt sie: „Oh, wir haben auch eine Familienpackung. Darin sind 2.400 g GummibĂ€rchen. Sie kostet 21 €. Vielleicht wollt ihr die zusammen nehmen?“

  1. Wie viel Gramm wĂŒrde jeder bekommen, wenn die TĂŒte gerecht aufgeteilt wird?
  2. Ist es dann fĂŒr jeden gĂŒnstiger?
    - Zeichne ein Koordinatensystem mit dem Graph B fĂŒr die Zuordnung: Anzahl der Mitglieder → Menge in g sowie den Graph C Anzahl der Mitglieder → anteiliger Preis in €
    -     Beantworte die Fragen.
  3. Vergleiche die Graphen A, B und C: Beschreibe AuffĂ€lligkeiten. BegrĂŒnde, warum sie die Graphen Ă€ußerlich unterscheiden.

Aufgabe

1. Beobachte die Entstehung der Graphen und erklÀre, was du erkennst.

2. Finde Unterschiede.

§

CC BY-SA 3.0

Urheber: PochtrÀger 

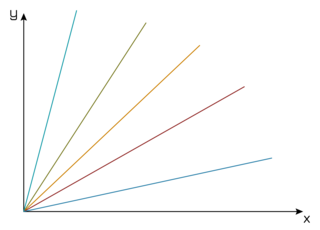
Quelle: https://www.geogebra.org/mater...
A B

3.2 Direkte ProportionalitÀt
3
§

Urheber: Digitale Lernwelten GmbH

Cc4BYNCSA

Eine Zuordnung heißt dann direkt proportional, wenn

  • die Verdopplung des Ausgangswertes (bzw. Verdreifachung, Vervierfachung usw.) dazu fĂŒhrt, dass auch der zugeordnete Wert verdoppelt (bzw. verdreifacht, vervierfacht usw.) wird;
  • die Halbierung des Ausgangswertes (bzw. Dritteln, Vierteln usw.) dazu fĂŒhrt, dass auch der zugeordnete Wert halbiert (bzw. gedrittelt, geviertelt usw.) wird.
4
 ? A B

Aufgabe – Wie entwickelt sich der Benzinpreis?

  1. Erforsche die Änderungen, wenn sich der Preis pro Liter und die getankte Menge in der Übung unten Ă€ndern.
  2. Formuliere 'Je-mehr-desto-mehr'-Aussagen zu dieser Aufgabe.
§

CC BY-SA 3.0

Urheber: holo 

Quelle: https://www.geogebra.org/material/show/id/dv68Bdtm

Aufgabe

Mia bestellt fĂŒr die neue Saison neue Trikots fĂŒr die Mannschaft. Ein Trikot kostet 32,50 €.

  1. Entscheide: Ist die Zuordnung Anzahl der Trikots → Preis in € proportional?
  2. ÜberprĂŒfe deine Entscheidung mit einer Tabelle.
A B

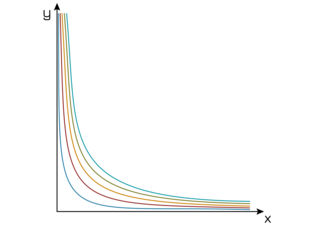
3.3 Indirekte ProportionalitÀt
5
§

Urheber: Digitale Lernwelten GmbH

Cc4BYNCSA

Eine Zuordnung heißt dann indirekt proportional, wenn

  • die Verdopplung des Ausgangswertes (bzw. Verdreifachung, Vervierfachung usw.) dazu fĂŒhrt, dass der zugeordnete Wert halbiert (bzw. gedrittelt, geviertelt usw.) wird.
  • das Halbieren des Ausgangswertes (bzw. das Dritteln, Viertel usw.) dazu fĂŒhrt, dass sich der zugeordnete Wert verdoppelt (bzw. verdreifacht, vervierfacht usw.).
6
 ? A B C

Aufgabe

  1. Bearbeite die Aufgabe.
  2. Formuliere 'Je-mehr-desto-weniger'- und 'Je-weniger-desto-mehr'-Aussagen.
§

CC BY-SA 3.0

Urheber: BeHe 

Quelle: https://www.geogebra.org/material/show/id/qmmqamrm

Aufgabe

  1. Löse die Rechenaufgabe unten.
  2. Kontrolliere deine Lösung, indem du dir den Graphen zeichnen lÀsst.
§

CC BY-SA 3.0

Urheber: GeoGebra Materials Team

Quelle: https://www.geogebra.org/m/dRmb2NYd

Aufgabe

Luna erklĂ€rt sich bereit, das Vereinsheim zu schmĂŒcken. Sie meint jedoch: „Wenn ich alles alleine dekorieren muss, brauche ich bestimmt 3 Stunden! Es wĂ€re nett, wenn mir noch zwei helfen wĂŒrden.“

Wie lange dauert es, das Vereinsheim zu dekorieren, wenn Ben und Laura mithelfen?
A B C

3.4 Direkt oder indirekt proportional?
7

Aufgabe

  1. Entscheide: Sind die Zuordnungen in den Tabellen direkt, indirekt oder gar nicht proportional?
  2. Übertrage die Zuordnungen in ein Heft und prĂŒfe deine Antwort mithilfe von Pfeilen.
  3. ErgÀnze die Tabellen um drei weitere Ausgangswerte.
8
Ausgangswert1,252,53,7556,257,5
zugeordneter Wert 2,33,64,96,27,58,8
9
Ausgangswert1234567
zugeordneter Wert 42021014010,5847060
10
Ausgangswert 1,534,567,5911,5
zugeordneter Wert 2,13,25,18,712,214,516
11
 ?
Welcher der Graphen zeigt eine direkte, indirekte oder gar keine proportionale Zuordnung? Ordne sie richtig ein.
12
 ?
Lies dir die Aufgaben durch. Entscheide, ob es sich um eine direkt oder indirekt proportionale Zuordnung handelt.