Du hast bereits gemerkt, dass π eine ganz besondere Zahl ist. Mit ihrer Hilfe kannst du den Umfang eines Kreises ausrechnen. Aber das ist noch nicht alles ...

§
Urheber: Digitale Lernwelten GmbH
3.1 Der Flächeninhalt eines Kreises
Wie kommt man auf die Formel für den Flächeninhalt eines Kreises?
Versuche, die einzelnen Pizzastücke im GeoGebra-Fenster so anzuordnen, dass eine Fläche entsteht, die du kennst. An den schwarzen Kreuzen kannst du sie bewegen, an den blauen können sie gedreht werden. Falls nötig, kannst du dir eine Hilfe einblenden lassen.
Stelle eine Vermutung auf, wie die Formel für den Flächeninhalt eines Kreises aussehen könnte.
§
CC BY-SA 3.0
Urheber: Sebastian Attenberger
Zusatz: Willst du es noch ein bisschen genauer erforschen?
Zusatz: Willst du es noch ein bisschen genauer erforschen?
§
CC BY-SA 3.0
Urheber: stellmich
Formel zur Berechnung des Flächeninhalts eines Kreises
Formel für den Flächeninhalt eines Kreises
Formel für den Flächeninhalt eines Kreises
Für den Flächeninhalt A eines Kreises mit dem Radius r gilt:
A = π * r2
Förderfenster: sinnvolle Skizzen erstellen
Dein Lehrer hat bestimmt schon gesagt: „Mach dir eine Skizze!“
Hast du diesen Rat befolgt?
Bestimmt nicht.
Das ist doch mehr Arbeit.
ABER: Skizzen können dir helfen und du kannst sogar Zeit sparen.
Du musst aber wissen, wie du sie anwendest.
Die Kreisfläche ist hierzu ein gutes Beispiel. Löse folgende Aufgabe:
Ein Kreis hat einen Radius von 2 cm. Berechne den Durchmesser und den Flächeninhalt.
Plötzlich hast du drei Begriffe und eine Zahl in der Aufgabenstellung. Dein Gehirn muss hier ganz schön arbeiten. Eine Skizze kann hier beim Denken helfen.
Aber wie funktioniert das denn jetzt? Eine Skizze machen?
Bei einer sinnvollen Skizze werden alle Informationen aus der Aufgabe verbildlicht.
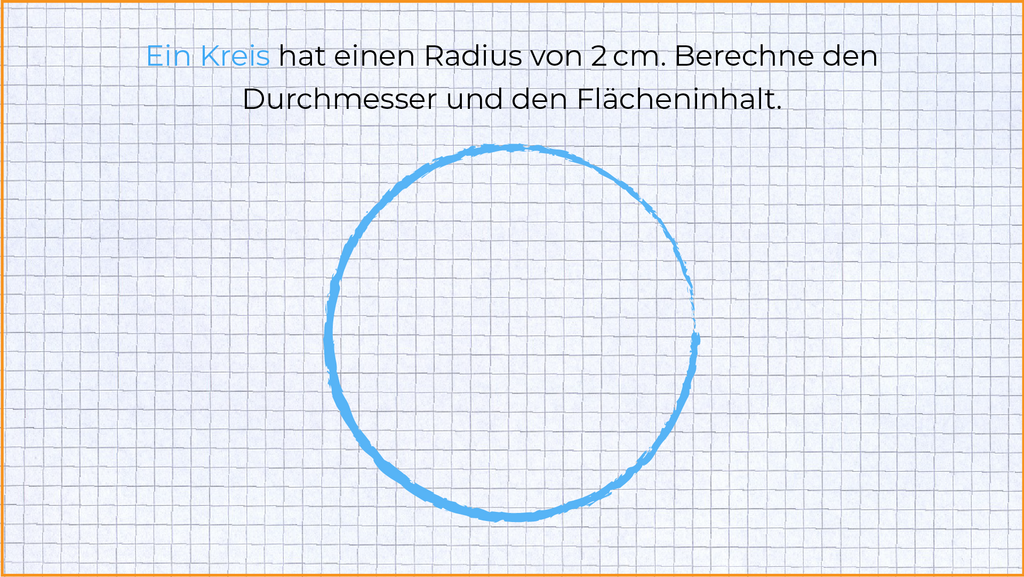
§
Urheber: Digitale Lernwelten GmbH
Durchsuche die Aufgabe nach allem, was gegeben ist.
Gegeben ist ein Kreis, also zeichnest du einen Kreis.
Der darf auch schief sein.
§
Urheber: Digitale Lernwelten GmbH
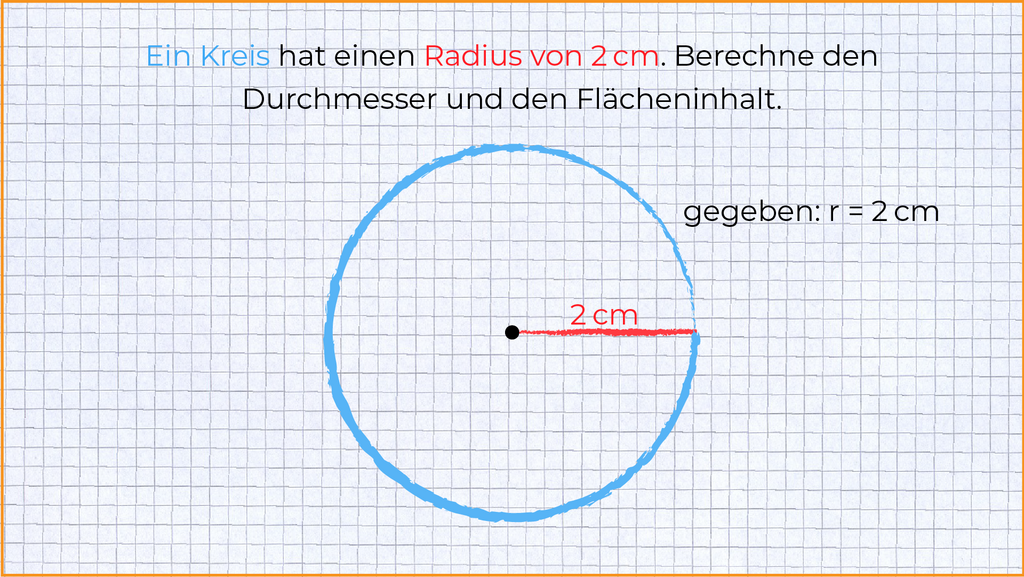
Gegeben ist ein Kreis mit einem Radius von 2 cm. Diese Information zeichnest du ein.
§
Urheber: Digitale Lernwelten GmbH
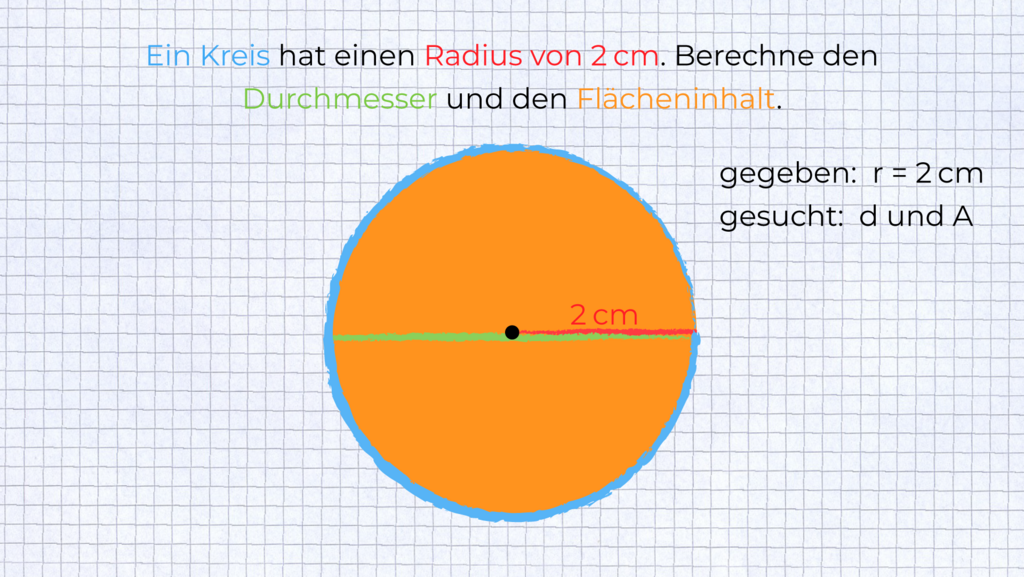
Als Nächstes fragst du dich wieder, was gesucht ist und zeichnest es ein.
Jetzt siehst du alle wichtigen Informationen.
§
Urheber: Digitale Lernwelten GmbH
Gesucht ist die grüne Linie (Durchmesser) und der Flächeninhalt (Fläche orange).
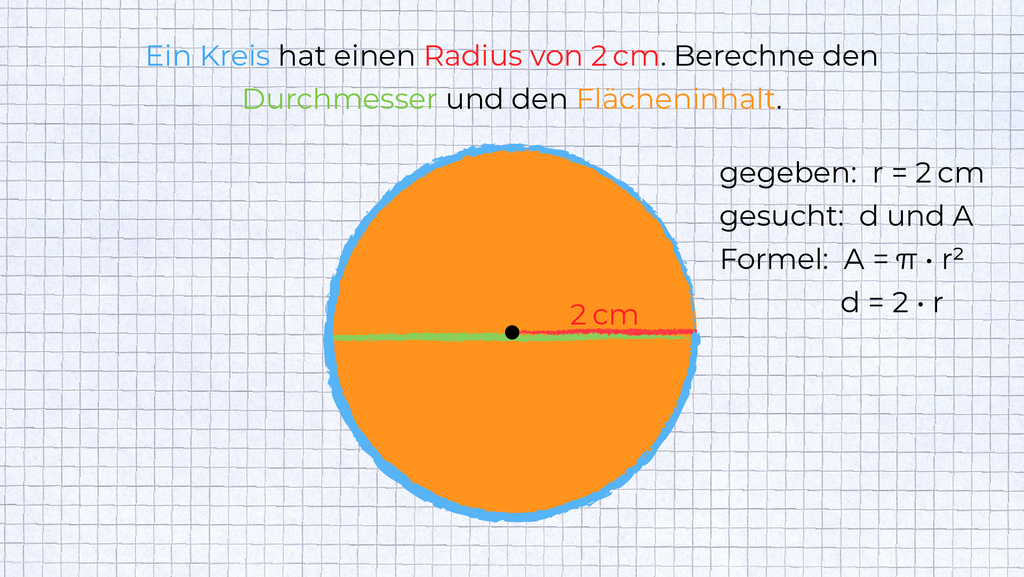
Welche Formel brauchst du, um die gesuchten Größen zu berechnen? Notiere!

§
Urheber: Digitale Lernwelten GmbH
Berechne den Durchmesser. Gehe Schritt für Schritt vor.

§
Urheber: Digitale Lernwelten GmbH
Berechne nun den Flächeninhalt. Gehe Schritt für Schritt vor.
Jetzt bist du dran:
Ein Kreis hat einen Radius von 3 cm. Mache eine Skizze.
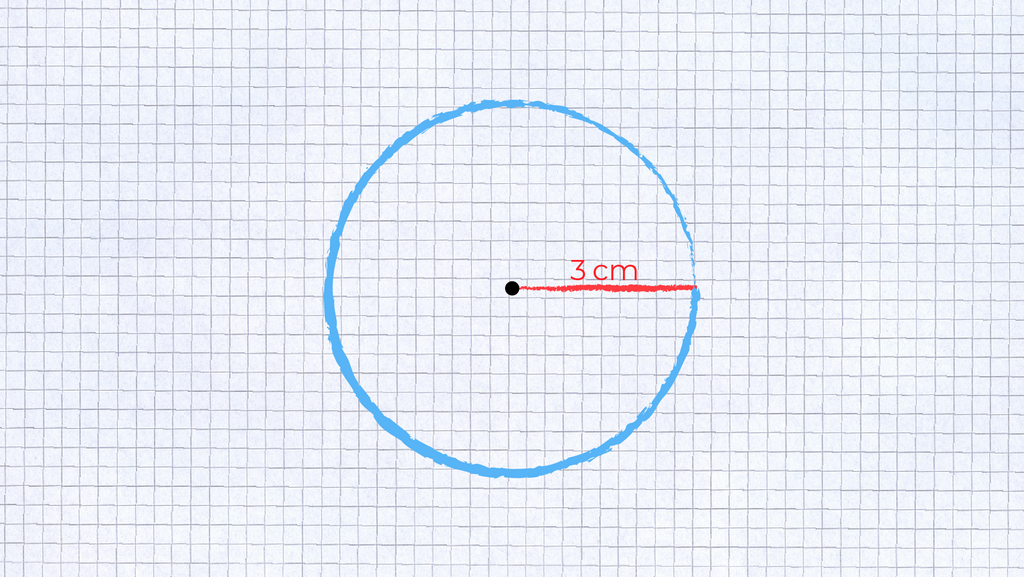
§
Urheber: Digitale Lernwelten GmbH
Berechne den Durchmesser und den Flächeninhalt.
Zeichne beides in die Skizze ein.
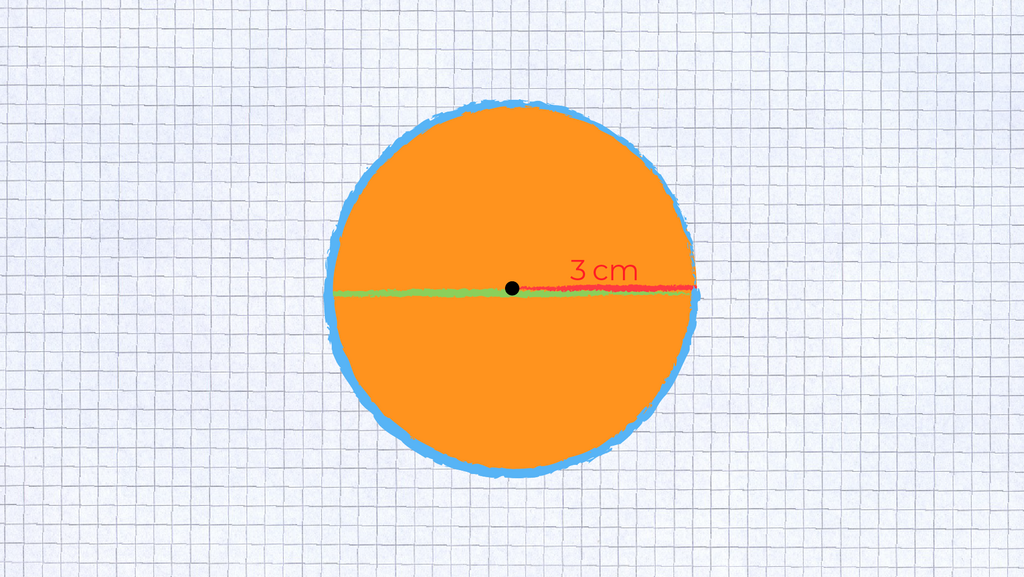
§
Urheber: Digitale Lernwelten GmbH
Notiere die gegebenen Größen und berechne.
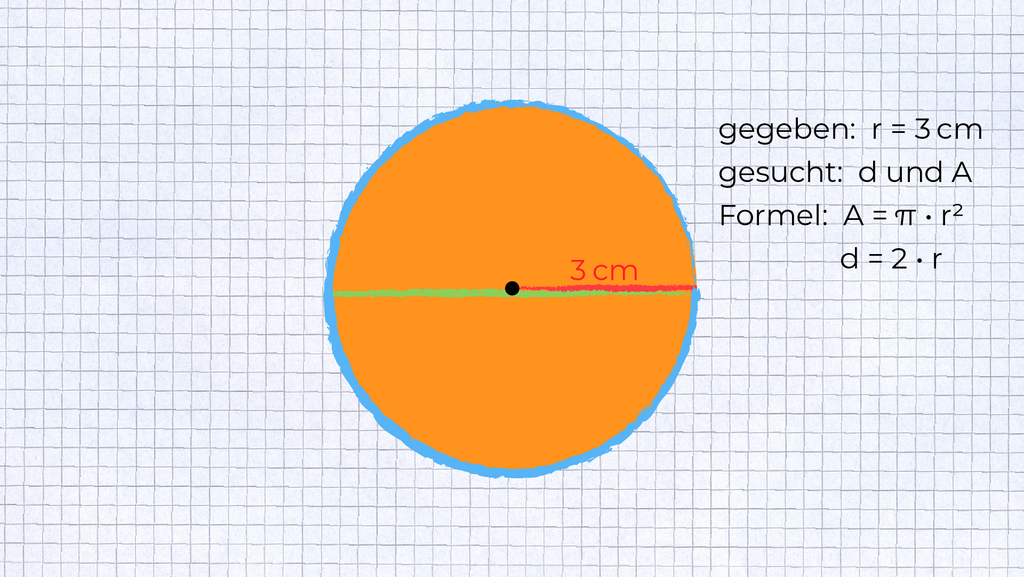
§
Urheber: Digitale Lernwelten GmbH
Text:
Gehe Schritt für Schritt vor.
Rechnung
Durchmesser:
d = 2 * 3 cm
d = 6 cm
Flächeninhalt:
A = π * r²
A = 3,14 * (3 cm)²
A = 28,26 cm²
Antwortsatz: Der Durchmesser beträgt 6 cm, der Flächeninhalt 28,26 cm².
Jetzt du ganz allein. Löse die Aufgabe, genau wie die beiden davor. Mache eine Skizze.
Ein Kreis hat einen Radius von 4 cm. Berechne Durchmesser und Flächeninhalt.
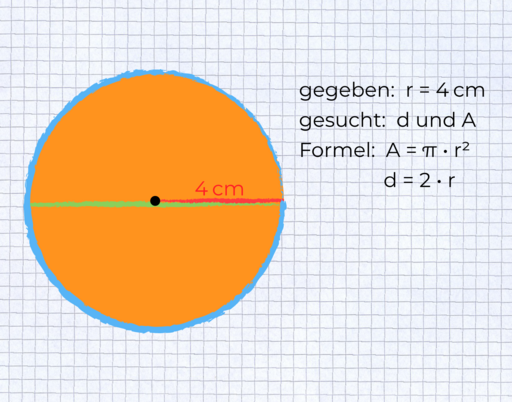
§
Urheber: Digitale Lernwelten GmbH
Rechnung
Durchmesser:
d = 2 * 4 cm
d = 8 cm
Flächeninhalt:
A = π * r²
A = 3,14 * (4 cm)²
A = 50,24 cm²
Antwortsatz: Der Durchmesser beträgt 8 cm, der Flächeninhalt 50,24 cm².
Rechne mit π = 3,14 (nicht die Taste auf deinem Taschenrechner). Runde dein Ergebnis auf zwei Nachkommastellen.
Aufgabe

§
Urheber: Unsplash
Der Mittelkreis eines Fußballfeldes hat einen Radius von 9,15 m.
Wie groß ist der Flächeninhalt dieses Mittelkreises?
Aufgabe
Eine Drohne hat eine Reichweite von 25 m. Wie groß ist das kreisförmige Gebiet, welches sie abfliegen könnte?

§
Urheber: AlLes
Pixabay
...
Jetzt sind die Profis gefragt
3.2 Der Flächeninhalt eines Kreisringes
Manchmal wollen wir nicht die komplette Fläche berechnen, sondern nur einen Teil. In diesem Fall die blau gefärbte Fläche. Diese wird wegen ihrer Form auch Kreisring genannt.
Wie könnte man eine solche Fläche berechnen? Hast du eine Idee?
§
CC BY-SA 3.0
Urheber: GeoGebra Translation Team German
Formel zur Berechnung eines Kreisringes
Formel für den Flächeninhalt eines Kreisringes
Formel für den Flächeninhalt eines Kreisringes
A Kreisring = A groß - A klein
A Kreisring= rgroß2 * π - rklein2 * π
= > A Kreisring = π * (rgroß2 - rklein2)
Aufgabe
Zeichne um einen Mittelpunkt M zwei Kreise. Kreis1 hat einen Radius von 2 cm, Kreis2 hat einen Radius von 6 cm.
a.) Färbe die Ringfläche bunt ein.
b.) Berechne die Fläche, die du eben eingefärbt hast.
Förderfenster: Größensalat
§
Urheber: Digitale Lernwelten GmbH
Übe die Schritte zur Bearbeitung einer Textaufgabe.
Notiere für jedes Beispiel:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.

§
Urheber: Digitale Lernwelten GmbH
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
Lösung:
Gegeben: r = 6,5 cm
Gesucht: Flächeninhalt
Formel: A = π *r²
Setze in die Formel ein: A = π * 6,5 cm²
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
A = 94,99 cm²
r = 5,5 cm
d = 11 cm
Lösung:
Gegeben: d = 11 cm
Gesucht: Umfang
Formel: u = π * d
Setze in die Formel ein: u = π * 11 cm
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
Ein Kreis hat einen Umfang von 62 cm, einen Durchmesser von 20 cm und einen Radius von 10 cm.
Lösung:
Gegeben: r = 10 cm
Gesucht: Flächeninhalt
Formel: A = π * r²
Setze in die Formel ein: A = π * 10 cm²
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
r = 3 mm
d = 6 mm
A = 28,26 mm²
Lösung:
Gegeben: d = 6 mm
Gesucht: Umfang
Formel: u = π * d
Setze in die Formel ein: u = π * 6 mm
§
Urheber: Digitale Lernwelten GmbH
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
Lösung:
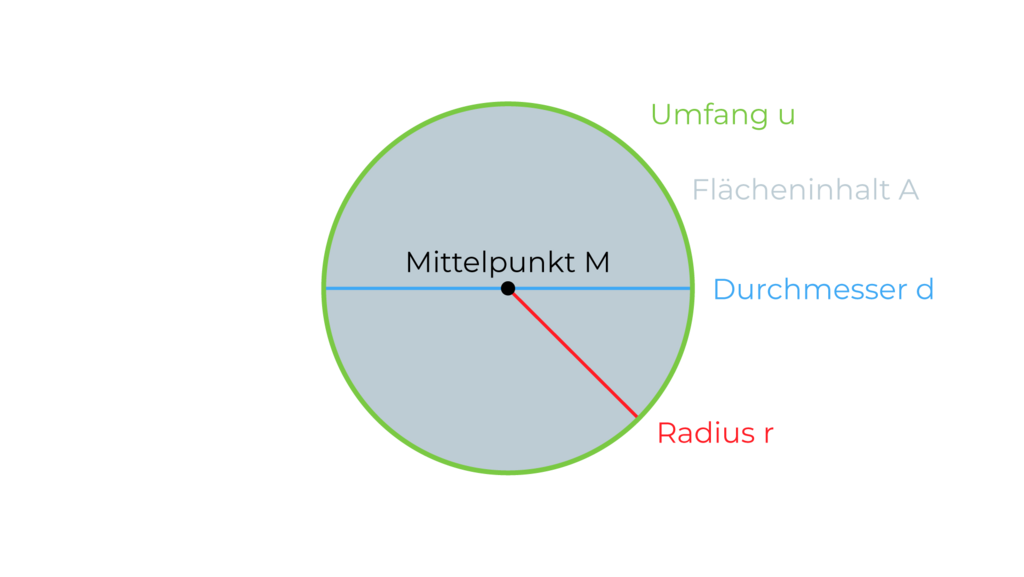
Gegeben: r = 7,5 cm
Gesucht: Durchmesser
Formel: d = r * 2
Setze in die Formel ein: d = 7,5 cm * 2
§
Urheber: Digitale Lernwelten GmbH
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
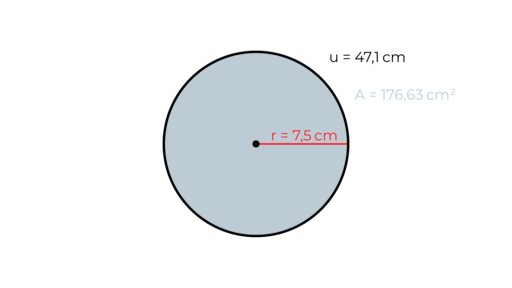
Lösung:
Gegeben: d = 4,5 cm
Gesucht: Radius
Formel: r = d : 2
Setze in die Formel ein: r = 4,5 cm : 2
Notiere:
- Was ist gegeben?
- Was ist gesucht?
- Wie lautet die Formel?
- Setze in die Formel ein.
Ein Kreis hat einen Radius r von 13,2 m. Einen Flächeninhalt von 547,1 m² und einen Umfang von 82,9 m.
Lösung:
Gegeben: r = 13,2 m
Gesucht: Durchmesser
Formel: d = r * 2
Setze in die Formel ein: d = 13,2 m * 2
Wie viele dieser 7 Aufgaben hast du richtig gelöst?
6 und mehr? Glückwunsch!
5 oder weniger? Da musst du noch mal üben.
Aufgabe

§
Urheber: Jjuni
Pixabay
Das Rad eines Autos hat einen Durchmesser von 801 mm. Die Felgen haben einen Durchmesser von 16 Zoll (1 Zoll = 2,54 cm). Wie breit sind die Reifen?
Aufgabe

§
Urheber: Unsplash
Das komplette Beet hat einen Radius von 5 m. Der innere Kreis, der nur aus weißen Blumen besteht, hat einen Radius von 2 m.
a.) Der äußere Kreis des Beetes soll neu bepflanzt werden (lila und rosa Blumen). Dazu muss der Gärtner wissen, wie groß die Fläche dieses Kreisrings ist. Berechne.
b.) Pro Quadratmeter möchte der Gärtner vier Blumensträucher einpflanzen. Wie viele muss er dafür im Baumarkt kaufen? Runde auf eine ganze Zahl.
Aufgabe

§
Urheber: Matteo Orlandi
Pixabay
Überlege dir eine Aufgabe zur Berechnung von Kreisflächen passend zum Bild. Stelle diese Aufgabe deinem Partner.