3. Winkelbeziehungen

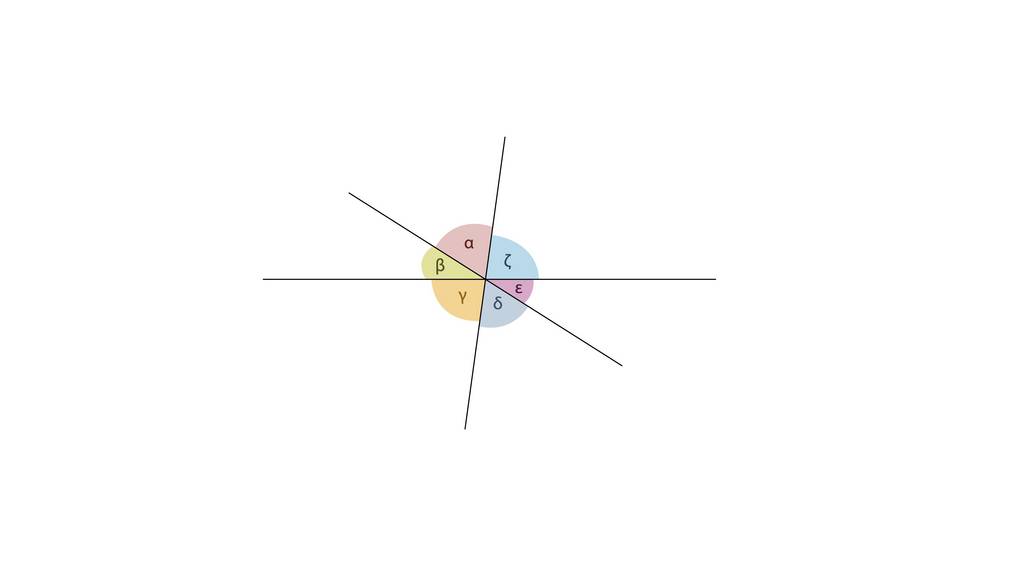
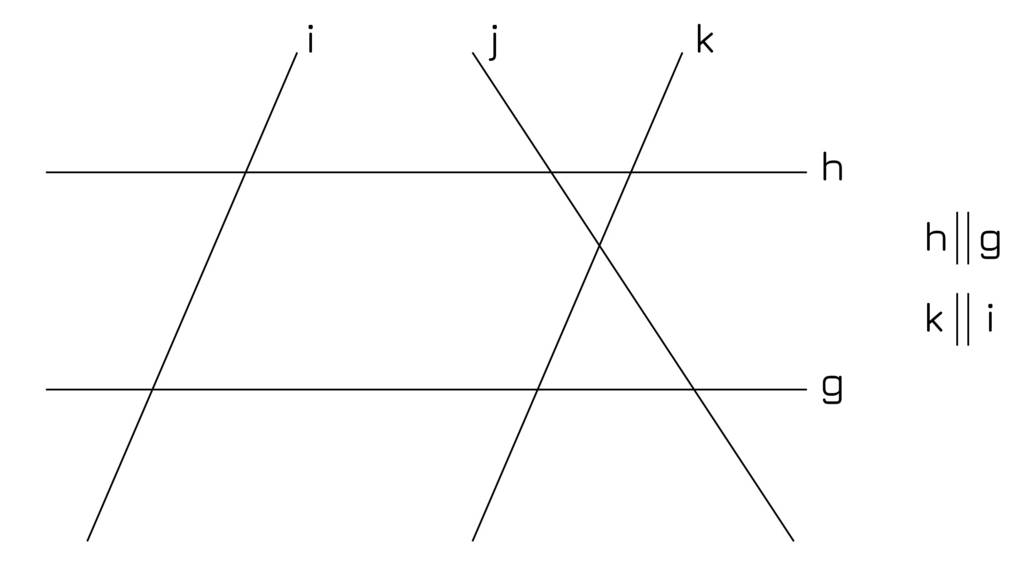
Nimm dir ein Stück Papier, eine Ecke reicht. Falte dieses Stück nun zweimal so, dass durch die Faltlinien eine Geradenkreuzung entsteht. Wie viele Winkel sind nun entstanden? Miss sie.

Falte das Papier nun so, dass die neue Faltlinie senkrecht (also im rechten Winkel) zu einer anderen steht. Wie viele Winkel hast du nun erhalten?

Falte nun noch einmal parallel zu einer anderen Faltlinie. Wie viele Winkel kannst du jetzt zählen?

Vergleiche dein Blatt mit dem deines Nachbarn. Habt ihr Ähnlichkeiten oder Unterschiede in euren Blättern? Ist euch etwas Besonderes aufgefallen?

3.1 Neben- und Scheitelwinkel

Nebenwinkel

In der Übung unten siehst du zwei Winkel. Dies sind sogenannte 'Nebenwinkel'. Verschiebe die Geraden und versuche eine Regel für 'Nebenwinkel' aufzustellen und diese zu begründen.

CC BY-SA 3.0

Urheber: Birgit Lachner

Quelle: https://www.geogebra.org/m/DUNktpEg

Scheitelwinkel

In der Übung unten siehst du zwei Winkel. Dies sind sogenannte 'Scheitelwinkel'. Verschiebe die Geraden und versuche eine Regel für 'Scheitelwinkel' aufzustellen und diese zu begründen.

CC BY-SA 3.0

Urheber: Birgit Lachner

Quelle: https://www.geogebra.org/m/VzsHg2zT

Was hast du herausgefunden? Merke

1.) Bei zwei sich schneidenden Geraden sind die gegenüberliegen Winkel immer gleich groß. Man nennt sie Scheitelwinkel.

Urheber: Birgit Lachner

Quelle: https://www.geogebra.org/m/Vzs...

2.) Bei zwei sich schneidenden Geraden, bilden zwei Winkel die nebeneinander liegen, immer einen gestreckten Winkel. Sie sind also 180° groß. Man nennt sie Nebenwinkel.

Urheber: Birgit Lachner

Quelle: https://www.geogebra.org/m/DUN...

3.2 Stufen- und Wechselwinkel

Die dritte Gerade

Wenn sich zwei Geraden schneiden, entstehen Neben- und Wechselwinkel. Was passiert nun, wenn eine dritte Gerade hinzukommt, die parallel zu einer der bereits vorhandenen verläuft?

Bewege den grünen Schieberegler und stelle eine Vermutung auf. Klicke im Tab dann auf B, um weiter zu machen.

CC BY-SA 3.0

Urheber: Christian Sänger

Quelle: https://www.geogebra.org/m/uK8rU8wM

Stufenwinkel

Kommt eine dritte gerade hinzu, entstehen neue Winkel.

Was ist das besondere an diesen neuen Winkeln? Bewege den grünen Punkt, um eine Vermutung aufzustellen.

CC BY-SA 3.0

Urheber: Wollny

Quelle: https://www.geogebra.org/m/tujda4da

Stufenwinkel

Du hast bestimmt herausgefunden, dass bei einer dritten Gerade neue Winkel entstehen, die genau so groß sind, wie die vorherigen. Hierfür gibt es jedoch eine Bedingung. Welche könnte das sein? Klicke hierzu in das Kästchen.

CC BY-SA 3.0

Urheber: Wollny

Quelle: https://www.geogebra.org/m/tujda4da

Was hast du herausgefunden? Merke

Wenn zwei Parallelen von einer Gerade geschnitten werden, entstehen sogenannte Stufenwinkel. Sie liegen, wie auf Stufen, auf oder unter den Parallelen und sind gleich groß.

Klicke auf das Kästchen 'Stufenwinkel' und ziehe am Schieberegler, um dir alle Stufenwinkel anzeigen zu lassen.

CC BY-SA 3.0

Urheber: Birgit Lachner

Quelle: https://www.geogebra.org/m/Mbw...

Wechselwinkel

Ich behaupte, dass der grüne und der blaue Winkel ebenfalls gleich groß sind. Verschiebe den grünen Winkel α und begründe, ob ich recht habe oder nicht. Klicke dann im Tab auf B, um weiterzumachen.

CC BY-SA 3.0

Urheber: Wollny

Quelle: https://www.geogebra.org/m/yuxyveba

Wenn man den Winkel α verschiebt, verändert sich seine Größe nicht. Es entsteht ein Stufenwinkel. Außerdem hast du gesehen, dass α durch die Verschiebung zum Scheitelwinkel von β wird.

α und β sind also ebenfalls gleich groß. Man nennt sie Wechselwinkel.

CC BY-SA 3.0

Urheber: Wollny

Quelle: https://www.geogebra.org/m/yuxyveba

Was hast du herausgefunden? Merke

Wenn zwei Parallelen von einer Gerade geschnitten werden, entstehen sogenannte Wechselwinkel. Im Unterschied zu den Stufenwinkel, liegen Wechselwinkel auf der linken und rechten Seite der Gerade.

Klicke auf das Kästchen 'Wechselwinkel' und ziehe am Schieberegler, um dir alle Wechselwinkel anzeigen zu lassen.

CC BY-SA 3.0

Urheber: Birgit Lachner

Quelle: https://www.geogebra.org/m/Mbw...

Trainiere deine Vorstellungskraft

Fällt es dir schwer, dir vorzustellen, dass Stufen- und Wechselwinkel immer gleich groß sind? Bewege die markierten Stellen und beobachte, was passiert.

CC BY-SA 3.0

Urheber: Stempfle, Ulrike Kempfle

Quelle: https://www.geogebra.org/m/svn...

Aufgabe A

Um welche Winkel handelt es sich hier und was sind ihre Eigenschaften? Ordne die Textschnipsel der richtigen Zeichnung zu.

Aufgabe B

Um welche Winkel handelt es sich hier und was sind ihre Eigenschaften? Ordne die Textschnipsel der richtigen Zeichnung zu.

Aufgabe C

Finde die verschiedenen Winkelbeziehungen auf deinem Stück Papier.

Notiere dir die verschiedenen Winkelbeziehungen mit jeweils einem Beispiel in dein Heft.

Aufgabe D

Berechne die Größe der übrigen Winkel.

a.) α= 127° und β= 15°

b.) δ= 57° und γ= 108°

c.) β= 90° und γ= 33°

d.) α= 109° und ε= 16°

Aufgabe E

Übertrage die Figur in dein Heft. Markiere gleich große Winkel mit derselben Farbe.

Aufgabe F

Übertrage die folgenden Winkel in dein Heft. Zeichne zu jedem den entsprechenden Scheitel- sowie die Nebenwinkel und beschrifte sie.

a.) α= 75°
b.) α= 48°
c.) α= 110°
d.) α= 95°
e.) α= 66°
f.) α= 145°

Aufgabe A

Aufgabe B

Gegeben seien die folgenden Winkel. Zeichne jeden dieser Winkel in dein Heft und ergänze die Darstellung durch einen Stufen- und zwei Wechselwinkel.

a.) α= 35°
b.) α= 72°
c.) α= 96°
d.) α= 102°

Aufgabe C

Zeichne zwei Parallelen und eine Gerade, welche die Parallelen schneidet. Erstelle selbst eine Aufgabe zu deiner Abbildung und stelle sie deinem Partner.

Aufgabe D

Aufgabe E

Bestimme die fehlenden Winkel und überprüfe sie anschließend.

CC BY-SA 3.0

Urheber: Ulrike Kempfle

Quelle: https://www.geogebra.org/m/BTzsVVMm