KOPIE 1. Beurteilen von Bewegungen

Stell Dir vor, Du fährst mit dem Fahrrad.

Der Radweg ist auch für Fußgänger und vor Dir läuft eine langsame Fußgängerin.

Du willst überholen, aber dafür musst Du auf die Straße wechseln.

Hinter Dir kommt ein Auto.

Wie schnell musst Du sein, damit Du die Fußgängerin überholen kannst und das Auto nicht abbremsen muss?

In diesem Kapitel schauen wir uns an, wie man Bewegungen messen, dokumentieren und beurteilen kann.

1.1 Bewegungen im Alltag

In diesem Beispiel sind drei Körper in Bewegung.

der Fahrradfahrer

die Fußgängerin

das Auto

Wie weit ist das Auto noch entfernt?

Wann wird es den Fahrradfahrer einholen?

Im Alltag werden diese Werte häufig nur geschätzt.

Es gibt jedoch viele Bereiche, in denen man die Bewegungen genau beurteilen muss.

In manchen Situationen ist es wichtig, Bewegungen genau zu beurteilen. Schau dir diese Galerie an, um einige Beispiele zu entdecken.

Aufgabe A – Bewegungen im Alltag

Schau dir die Fotos an und beantworte folgende Fragen:

Welche Körper sind in Bewegung?
Warum ist es wichtig, die Bewegung dieser Körper genau zu beurteilen?

Aufgabe B – Weitere Bewegungen im Alltag

Finde weitere Beispiele aus Deinem Alltag!

Arbeite mit deinen Mitschülern zusammen.

Erstellt eine gemeinsame Liste.

1.2 Bewegungen dokumentieren

Bewegung findet statt, wenn ein Körper mit der Zeit seinen Ort ändert. Um die Bewegung zu dokumentieren, müssen zwei Größen beobachtet werden:

Wenn du für jeden Zeitpunkt feststellst, an welchem Ort sich ein Körper gerade befindet, kannst du die Bewegung des Körpers vollständig dokumentieren. Stell dir vor, ein Auto fährt auf einer Straße, an der ein riesiges Maßband angebracht ist – wie in der folgenden Animation zu sehen:

ANMERKUNG FÜR ELEMENT 6 UND 7

Animation und Tabelle: nur 10 Zeitpunkte und kein Hin-und zurückfahren, nur
geradeaus fahren und gleiche Strecken zu gleicher Zeit. Auch keine zwei Nullen am Anfang!

Wenn du für jede Sekunde den Weg notierst, den das Auto zurückgelegt hat, erhältst du eine vollständige Dokumentation der Bewegung.

Aufgabe – Bewegungen dokumentieren

Schau dir noch einmal das Video an und trage in der folgenden Tabelle für jede Zeit (t) in Sekunden (s) den Weg (s) in Metern (m) ein.

„t in s“ bezeichnet die Zeit in Sekunden
„s in m“ bezeichnet den Weg in Metern

Wähle für die Angaben des zurückgelegten Weges immer den Ort der vorderen Stoßstange des Autos.

1.3 Berechnung der Geschwindigkeit

Die Geschwindigkeit gibt an, wie schnell oder wie langsam ein Körper sich bewegt. Das Formelzeichen für die Geschwindigkeit ist v.

Man rechnet:

Geschwindigkeit = Weg / Zeit

in Formelzeichen ist das:

v = s / t

Wenn ein Auto also in 5 Sekunden 25 Meter zurücklegt, hat es eine Geschwindigkeit von

v = 25m / 5 s = 5 m/s.

In der Physik benutzt man als Einheit meist Meter pro Sekunde (m/s).

Im Straßenverkehr benutze man meist Kilometer pro Stunde (km/h).

Eine Bewegung, bei der die Geschwindigkeit immer gleich bleibt, nennt man gleichförmig. (Dazu im nächsten Kapitel mehr).

ACHTUNG NOCH NICHT VOLLSTÄNDIG

Erweiterung

Umrechnung von Meter pro Sekunde in Kilometer pro Stunde

Bestimmt ist dir bekannt, dass Geschwindigkeiten häufig auch in Kilometer pro Stunde (km/h) angegeben werden, z. B. bei Tempolimits im Straßenverkehr. Doch wie funktioniert die Umrechnung von km/h in m/s und andersherum?

1 Kilometer (km) sind 1000 Meter (m)
1 Stunde (h) sind 3600 Sekunden (s)

Daraus ergibt sich folgende Rechnung:

1 m/s = 3600 m / 3600 s = 3,6 km/h

1 m/s entspricht also 3,6 km/h. Um eine Geschwindigkeit von m/s in km/h umzurechnen, muss diese mit dem Faktor 3,6 multipliziert werden.

Für die Umrechnung von km/h zu m/s muss die Geschwindigkeit durch den Wert 3,6 geteilt werden.

Bonusaufgabe – Umrechnung von m/s und km/h

Berechne für die folgenden Geschwindigkeiten jeweils die Geschwindigkeit in m/s bzw. in km/h:

36 km/h
15 m/s
97,2 km/h
24 m/s
7 m/s
46,8 km/h

Infobox

Kilometer pro Stunde oder „Ka-em-ha“?

In der Umgangssprache sagt man oft kmh – gesprochen „Ka-em-ha“ anstatt „Kilometer pro Stunde“. Das ist aber nicht korrekt! Richtig heißt es „Kilometer pro Stunde“. Das „pro“ darf man nicht weglassen. Es macht klar, dass wir es mit einer Geteilt-Rechnung (Division) zu tun haben.

Aufgabe A – Formelzeichen und Einheiten

Du hast im Laufe des Kapitels bereits einige Größen kennengelernt: die Zeit, den Weg und die Geschwindigkeit. Jede hat ihr eigenes Formelzeichen und wird in bestimmten Einheiten angegeben. Ordne diese den richtigen Größen zu.

Aufgabe B – Je-desto-Aussagen

Weg, Zeit und Geschwindigkeit stehen in einem direkten Verhältnis zueinander: Wie verändert sich die Zeit, wenn derselbe Weg mit einer höheren Geschwindigkeit zurückgelegt wird? Wie verändert sich die Geschwindigkeit, wenn ein längerer Weg in derselben Zeit zurückgelegt werden muss?

Diese Abhängigkeiten können mit „Je-desto-Aussagen“ beschrieben werden. Lies dir die Sätze genau durch und vervollständige die Aussagen.

Erweiterung

Berechnung des Weges

Wenn die Geschwindigkeit eines Körpers und die zeitliche Dauer der Bewegung bekannt sind, kann daraus der Weg berechnet werden, den der Körper zurücklegt.

Erweiterung

Berechnung der Zeit

Wenn die Geschwindigkeit eines Körpers und der zurückgelegte Weg bekannt sind, kann daraus die zeitliche Dauer der Bewegung berechnet werden.

Ein Körper bewegt sich gleichförmig mit einer Geschwindigkeit (v) von 3 m/s und legt insgesamt einen Weg (s) von 30 Metern zurück. Da sich der Körper in jeder Sekunde um 3 Meter vorwärts bewegt, benötigt er für 30 Meter einen Zeitraum (t) von insgesamt 10 Sekunden.

Für die Berechnung der Zeit (t) wird der Weg (s) durch die Geschwindigkeit (v) geteilt.

t = s / v
t = 30 m / 3 m/s
t = 10 s

Zusammenfassung

Beurteilen von Bewegungen

1. Bewegungen dokumentieren

Bewegung findet statt, wenn ein Körper mit der Zeit seinen Ort ändert. Um Bewegungen zu dokumentieren, müssen zwei Größen beobachtet werden:

Die Zeit | Formelzeichen: t | Einheit: eine Sekunde (1 s)
Der Weg | Formelzeichen: s | Einheit: ein Meter (1 m)

Beispiel einer dokumentierten Bewegung:

t in s	0	1	2	3	4	5
s in m	0	2	4	4	7	10

4. Berechnung der Geschwindigkeit

Die Geschwindigkeit gibt an, in welcher Zeit t ein bestimmter Weg s zurückgelegt wird.

Die Geschwindigkeit | Formelzeichen: v | Einheit: ein Meter pro Sekunde (1 m/s)

Die Geschwindigkeit wird wie folgt berechnet:

v = s/t
v = 6 m / 2 s
v = 3 m/s

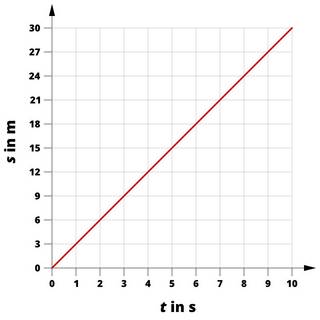
Der Körper bewegt sich in dem zuvor markierten Zeitabschnitt mit einer Geschwindigkeit von 3 m/s.

Eine höhere Geschwindigkeit bedeutet einen größeren Anstieg des Graphen im s(t)-Diagramm. Bei gleichförmigen Bewegungen ist der Anstieg des Graphen gleich der Geschwindigkeit des Körpers.

In manchen Fällen werden Geschwindigkeiten in km/h angegeben. Für die Umrechnung ergeben sich folgende Umrechnungsformeln:

1 m/s = 1 km/h * 3,6
1 km/h = 1 m/s / 3,6

Für die Berechnung des Weges werden Zeit und Geschwindigkeit miteinander multipliziert:

s = v * t

Für die Berechnung der Zeit wird der Weg durch die Geschwindigkeit geteilt.

t = s / v