In diesem Kapitel kannst du die Ermittlung von Wahrscheinlichkeiten noch etwas üben.

§
https://www.pexels.com/de-de/foto/hand-schreibtisch-laptop-notizbuch-4240497/
5. Zufallsversuche: Übungen
Aufgabe 1

§
© Digitale Lernwelten GmbH, erstellt mit Canva
Am Flughafen wird eine Gruppe von fünf Personen durch die Zollkontrolle geleitet. Obwohl alle angeben, in ihrem Amerikaurlaub nur Waren im erlaubten Warenwert eingekauft zu haben, haben Sven und Tim diesen Wert deutlich überschritten und schmuggeln somit Waren über die Grenze. Der Zollbeamte wählt zwei der fünf Personen aus, um sie zu durchsuchen.
- Mit welcher Wahrscheinlichkeit erwischt der Zollbeamte zwei Nicht-Schmuggler (N)?
- Mit welcher Wahrscheinlichkeit erwischt der Zollbeamte mindestens einen der beiden Schmuggler (S)?
Zeichne zuerst ein Baumdiagramm. Errechne dann die Wahrscheinlichkeiten für die beiden Aufgaben.
Lösung zur Aufgabe 1
Lösung zur Aufgabe 1
§
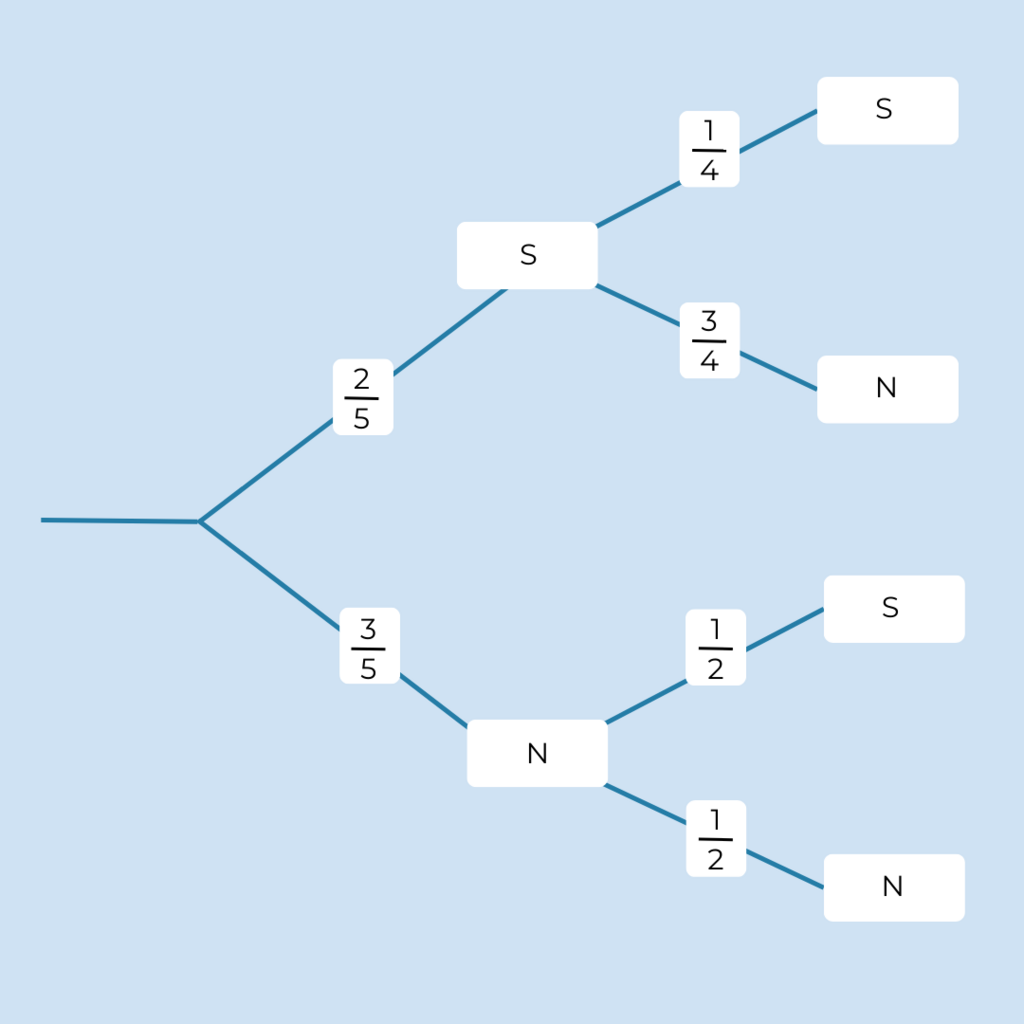
Hier siehst du den Baumgraphen zur Aufgabe.
Folgende Ergebnisse sind möglich:
S-S; N-S; S-N; N-N

§
Hier kannst du den jeweiligen Rechenweg nachvollziehen.
Aufgabe 2

§
Ein Multiple-Choice-Test besteht aus vier Fragen. Zu jeder der vier Fragen gibt es drei Antworten, davon ist nur eine Antwort richtig (r), zwei Antworten sind falsch (f). Jemand geht völlig unvorbereitet in den Test und kreuzt auf Glück an.
Wie groß ist die Wahrscheinlichkeit, dass die Person den Test besteht, wenn mindestens drei Fragen richtig angekreuzt sein müssen?
Zeichne zuerst ein Baumdiagramm und berechne im Anschluss die Wahrscheinlichkeit des Bestehens.
Lösung zur Aufgabe 2
Lösung zur Aufgabe 2
§
© Digitale Lernwelten GmbH
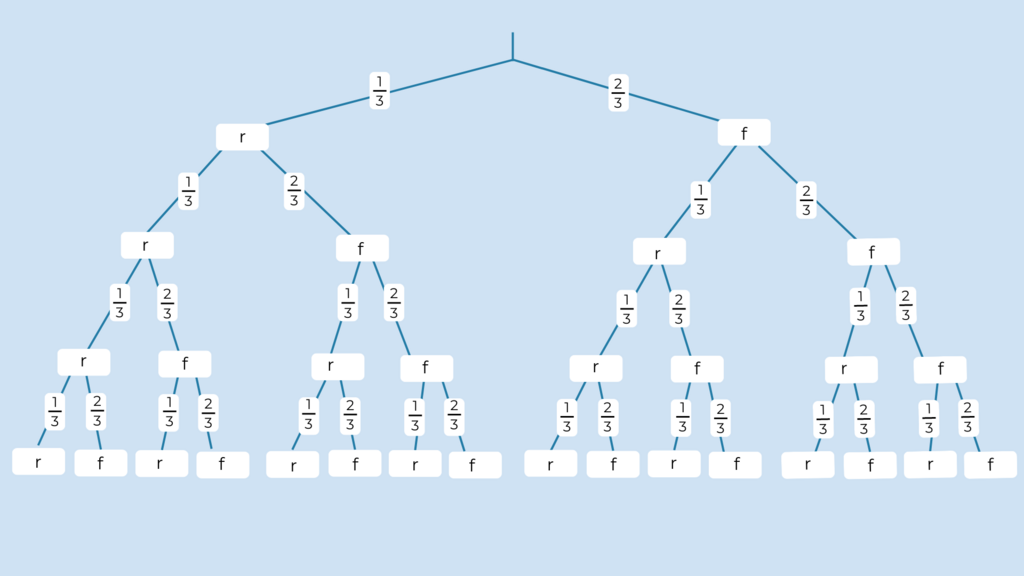
Hier siehst du das Baumdiagramm mit der Wahrscheinlichkeit des Ergebnisses, dass die Person den Test besteht.

§
Hier kannst du den Rechenweg nachvollziehen.
Aufgabe 3
§
© Digitale Lernwelten GmbH
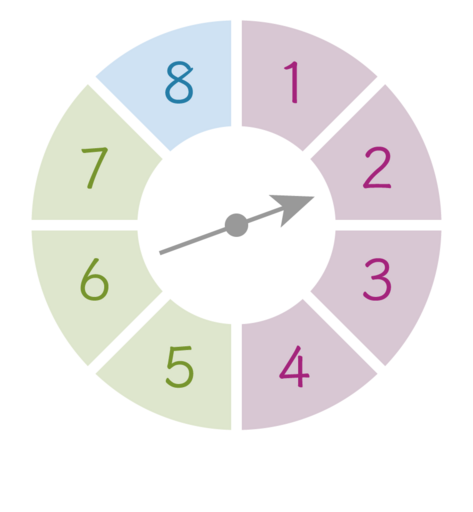
Das nebenstehende Glücksrad wird zweimal gedreht. Beim ersten Dreh wird nur die Zahl aufgeschrieben, beim zweiten Dreh die Farbe.
- Ist dieses Glücksrad „gerecht“? Überlege.
- Wie groß ist die Wahrscheinlichkeit einer blauen 8?
- Mit welcher Wahrscheinlichkeit erhält man bei zwei Drehungen eine grüne gerade Zahl?
Gib alle Wahrscheinlichkeiten als Bruchzahl an.
Lösung zu Aufgabe 3
Lösung zu Aufgabe 3

§
Aufgabe 4

§
© Digitale Lernwelten GmbH
In einem Behälter befinden sich vier weiße (W), eine schwarze (S) und zehn graue (G) Kugeln. Es werden nacheinander zwei Kugeln ohne Zurücklegen gezogen.
- Zeichne für diesen zweistufigen Zufallsversuch ein Baumdiagramm und beschrifte die Äste mit den jeweiligen Wahrscheinlichkeiten.
- Berechne die Wahrscheinlichkeit, dass man nach zweimaligem Ziehen eine graue und eine weiße Kugel erhält. Gib die Wahrscheinlichkeit auch in Prozent an.
- Berechne die Wahrscheinlichkeit, dass nach zweimaligem Ziehen mindestens eine der beiden gezogenen Kugeln grau ist. Gib die Wahrscheinlichkeit auch in Prozent an.
Lösung zu Aufgabe 4
Baumdiagramm
Lösung zu Aufgabe 4
Baumdiagramm
§
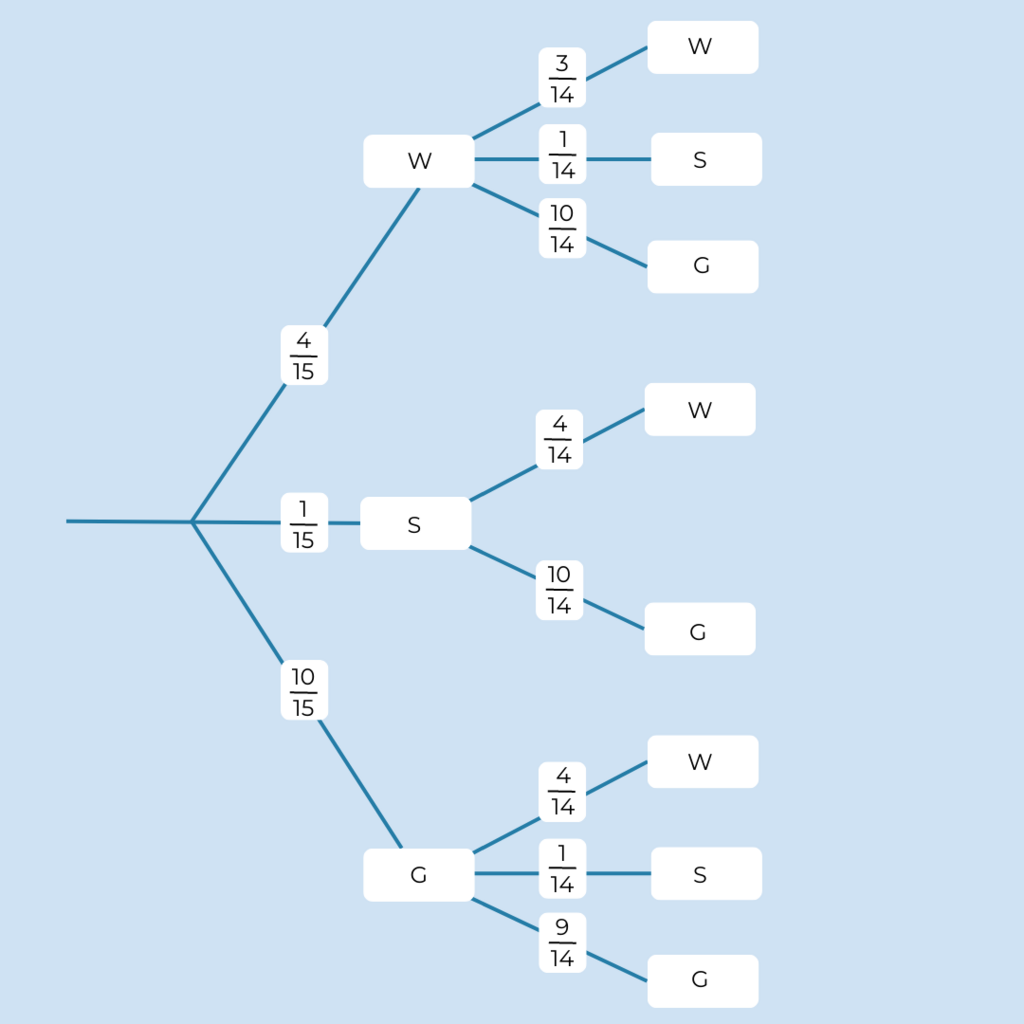
Hier siehst du das Baumdiagramm mit den jeweiligen Wahrscheinlichkeiten.

§
Hier kannst du den Rechenweg nachvollziehen.
Aufgabe 5
§
© Digitale Lernwelten GmbH
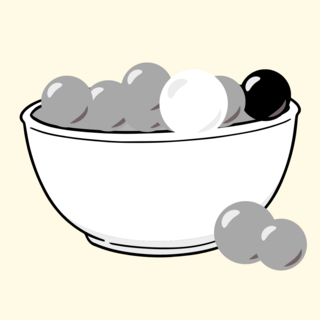
Der Zufallsversuch aus Aufgabe 4 wird nun wiederholt. Dieses Mal werden die Kugeln aber zurückgelegt.
Berechne jetzt die Wahrscheinlichkeit, dass nach zweimaligem Ziehen die gezogenen Kugeln die gleiche Farbe haben.
Fertige dir dazu als Hilfe vorab wieder ein Baumdiagramm an.
Lösung zu Aufgabe 5
Lösung zu Aufgabe 5
§
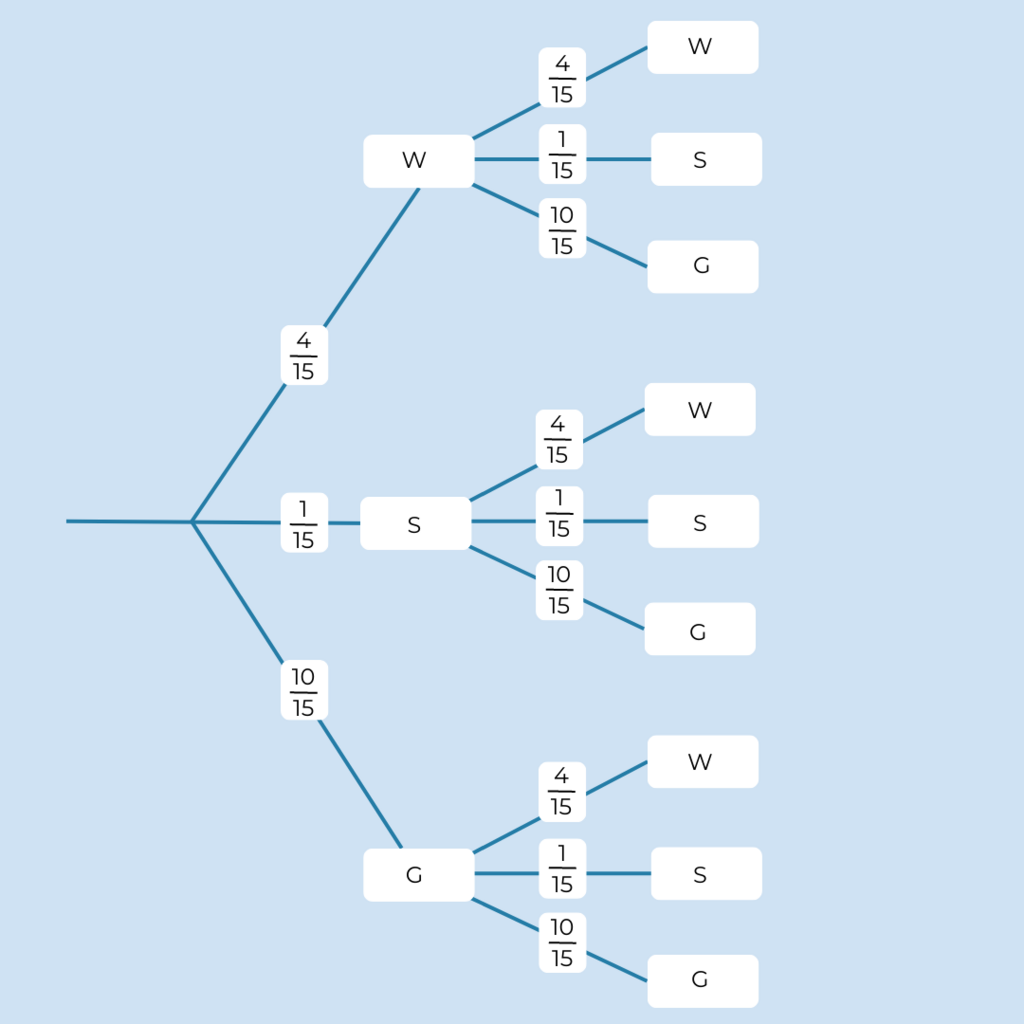
Hier siehst du das Baumdiagramm zur Aufgabe 5.
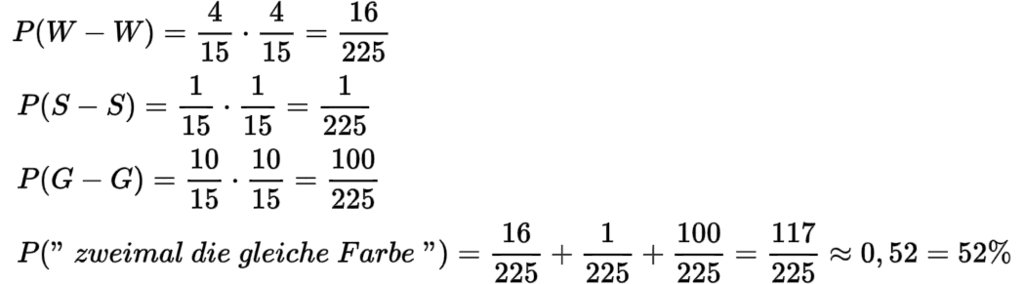
§
Hier kannst du den Rechenweg nachvollziehen.